Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
Mathematik-Online-Aufgabensammlung: Lösung zu

Aufgabe 1484: Differentialgleichungssystem.

A B C D E F G H I J K L M N O P Q R S T U V W X Y Z
a)
Bestimmen Sie die allgemeine reelle Lösung des Differentialgleichungssystems

$\displaystyle \begin{array} {rcr@{\hspace{0.2cm}}c@{\hspace{0.2cm}}r@ {\hspace{... ... \ y_1 & + & y_2 & - & y_3 \\ [0.1cm] y_3' & = & & & y_2 & - & y_3 \end{array} $

b)
Wie lautet die spezielle Lösung $ (y_1, y_2, y_3)$ mit $ y_1(0)=-9$, $ y_2(0)=7$ und $ y_3(0)=6$?

a)
Gegeben ist ein homogenes Differentialgleichungssystem erster Ordnung:

\begin{displaymath} \begin{array}{rcr@{\hspace{0.2cm}}c@{\hspace{0.2cm}}r@{\hspa... ... & - & y_3 \\ [0.1cm] y_3' & = & & & y_2 & - & y_3 \end{array}\end{displaymath}

das auch wie folgt geschrieben werden kann:

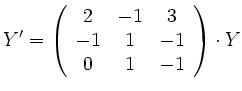
$\displaystyle Y'= \left(\begin{array}{ccc} 2&-1&3 \\ -1&1&-1 \\ 0&1&-1 \\ \end{array}\right)\cdot{Y} $

Um die allgemeine reelle Lösung zu bestimmen, müssen die Eigenwerte und die Eigenvektoren der obigen Matrix $ A$ berechnet werden.
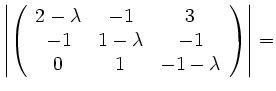$\displaystyle \det(A-\lambda \cdot E)$ $\displaystyle =$ $\displaystyle \left\vert \left( \begin{array}{ccc} 2-\lambda & -1 & 3 \\ -1 & 1-\lambda & -1 \\ 0 & 1 & -1-\lambda \\ \end{array}\right) \right\vert=$  
       
  $\displaystyle =$ $\displaystyle {}(2-\lambda)\cdot(1-\lambda)\cdot(-1-\lambda)+0-3-0+2-\lambda+1+\lambda=$  
  $\displaystyle =$ $\displaystyle {}(2-\lambda)\cdot(1-\lambda)\cdot(-1-\lambda)=0$  

Die Eigenwerte der Matrix $ A$ können bei dieser Gleichung abgelesen werden.

$ \lambda_{1}= 2$,          $ \lambda_{2}= 1$,          $ \lambda_{3}=-1$
Um die Eigenvektoren zu berechnen werden die Eigenwerte in folgendes Gleichungssystem eingesetzt


$\displaystyle \left(2-\lambda\right)y_1-y_2+3y_3$ $\displaystyle =$ 0  
$\displaystyle -1y_1+\left(1-\lambda\right)y_2-y_3$ $\displaystyle =$ 0  
$\displaystyle y_2+\left(-1-\lambda\right)y_3$ $\displaystyle =$ 0  

und dieses nach $ y_1$, $ y_2$ und $ y_3$ aufgelöst, die die jeweiligen Eigenvektoren zu den Eigenwerten ergeben. Für $ \lambda_1 = 2$ gilt:


$\displaystyle -y_2+3y_3$ $\displaystyle =$ 0  
$\displaystyle -y_1-y_2-y_3$ $\displaystyle =$ 0  
$\displaystyle y_2-3y_3$ $\displaystyle =$ 0  

$ \Rightarrow y_2=3y_3$ und $ y_1=-4y_3$ (durch auflösen) $ \Rightarrow$ der Eigenvektor für $ \lambda_1 = 2$ ist:

$\displaystyle EV_1=c_1\cdot \left(\begin{array}{c} -4 \\ \quad3 \\ \; 1 \\ \end{array}\right) $


Die anderen beiden Eigenvektoren können auf dieselbe Art und Weise bestimmt werden. Dadurch ergibt sich:

für $ \lambda_2 = 1$:

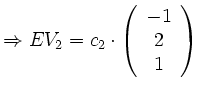
$\displaystyle \Rightarrow EV_2 = c_2\cdot \left(\begin{array}{c} -1 \\ 2 \\ 1 \\ \end{array}\right) $

für $ \lambda_3 = -1$:

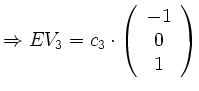
$\displaystyle \Rightarrow EV_3 = c_3 \cdot \left(\begin{array}{c} -1 \\ 0 \\ 1 \\ \end{array}\right) $

$ \Rightarrow$ die allgemeine Lösung für dieses Differentialgleichungssystem lautet:

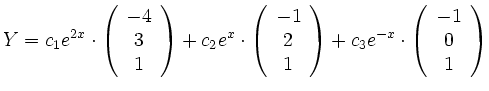
$\displaystyle Y=c_1e^{2x} \cdot \left(\begin{array}{c} -4 \\ 3 \\ 1 \\ \end{... ...t)+c_3e^{-x}\cdot \left(\begin{array}{c} -1 \\ 0 \\ 1 \\ \end{array}\right) $

b)
Hier soll mit den gegebenen Bedingungen die Konstanten $ c_1$, $ c_2$ und $ c_3$ berechnet werden.
Es wird sich wieder ein lineares Gleichungssystem ergeben, das nach den bekannten Methoden aufgelöst werden kann.


$\displaystyle y_1(0)$ $\displaystyle =$ $\displaystyle -4c_1-c_2-c_3 = -9$  
$\displaystyle y_2(0)$ $\displaystyle =$ $\displaystyle 3c_1+2c_2 = 7$  
$\displaystyle y_3(0)$ $\displaystyle =$ $\displaystyle c_1+c_2+c_3 = 6$  

$ \Rightarrow c_1=1$,        $ c_2=2$,        $ c_3=3$
Daraus folgt die spezielle Lösung:

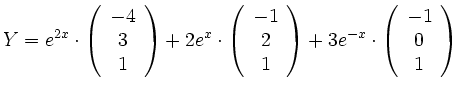
$\displaystyle Y=e^{2x}\cdot \left(\begin{array}{c} -4 \\ 3 \\ 1 \\ \end{arra... ...ght)+3e^{-x}\cdot \left(\begin{array}{c} -1 \\ 0 \\ 1 \\ \end{array}\right) $

(Prof. Dr. Eberhard Teufel, Dr. Norbert Röhrl)
[Zurück zur Aufgabe]
  automatisch erstellt am 17.  9. 2006