Schreiben Sie ein Programm spline_plot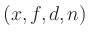 , das einen
kubischen Spline mit Knoten
, das einen
kubischen Spline mit Knoten 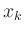 , Werten
, Werten 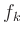 und Ableitungen
und Ableitungen 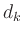 durch
Auswertung an
durch
Auswertung an 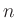 Punkten in jedem Intervall
Punkten in jedem Intervall
![$ \left[ x_k,
x_{k+1}\right]$](/inhalt/aufgabe/aufgabe1561/img6.png) graphisch darstellt.
graphisch darstellt.
function spline_plot(x,f,d,n)
% spline_plot(x,f,d,n)
% Plot eines Splines mit Knoten x
% Funktionswerten f, Ableitungen d
% mit n Punkten pro Intervall
% Vektoren zu Zeilen wandeln
x=x(:)';f=f(:)';d=d(:)';
% Auswertungspunkte auf Standardintervall in Spalte
s=linspace(0,1,n+1)';
% Auswertung der Lagrange-Polynome (Spalten)
ua=(1+2*s).*(1-s).^2;
va=s.*(1-s).^2;
ub=(3-2.*s).*s.^2;
vb=-s.^2.*(1-s);
% Vorfaktoren (Zeilen)
f_ua=f(1:end-1);
f_ub=f(2:end);
f_va=diff(x).*d(1:end-1);
f_vb=diff(x).*d(2:end);
% Auswertungspunkte (jedes Teilinterval eine Spalte)
X=repmat(x(1:end-1),n+1,1)+s*diff(x);
% Splinewerte (jedes Teilinterval eine Spalte)
F=ua*f_ua+ub*f_ub+va*f_va+vb*f_vb;
% plot (jedes Intervall seperate Kurve)
plot(X,F);
% plot (nur eine Kurve)
figure;
plot(X(:),F(:));
| |
automatisch erstellt
am 10. 12. 2007 |

