Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
Mathematik-Online:

Matrizen und lineare Gleichungssysteme

A B C D E F G H I J K L M N O P Q R S T U V W X Y Z Übersicht

Matrizen.

Sei $ K$ ein Körper. Seien $ m,n\geq 1$ . Eine Matrix $ A$ der Größe $ m\times n$ ist ein Tupel $ (a_{i,j})_{i\in\{1,\dots,m\},j\in\{1,\dots,n\}}$ von $ m\cdot n$ Elementen aus $ K$ , angeordnet in einer Tafel

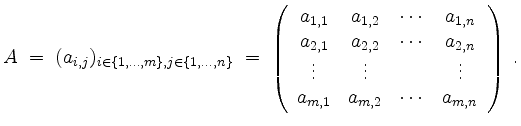
$\displaystyle A \;=\; (a_{i,j})_{i\in\{1,\dots,m\},j\in\{1,\dots,n\}} \;=\; \l... ...vdots & &\vdots \\ a_{m,1} & a_{m,2} & \cdots & a_{m,n} \end{array}\right)\;. $

Die Menge aller $ m\times n$ -Matrizen wird mit $ K^{m\times n}$ bezeichnet. Die Elemente $ a_{i,j}$ heißen die Einträge der Matrix $ A$ .

Matrizen der Größe $ m\times 1$ werden auch als Spaltenvektoren bezeichnet. Wir schreiben auch $ K^m:=K^{m\times 1}$ .

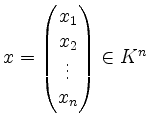Ist $ A = (a_{i,j})_{i\in\{1,\dots,m\},j\in\{1,\dots,n\}}\in K^{m\times n}$ und $ x=\begin{pmatrix}x_1\\ x_2\\ \vdots\\ x_n\end{pmatrix}\in K^n$ , so definiert man das Produkt von Matrix und Spaltenvektor durch

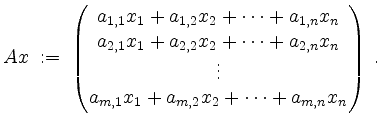
$\displaystyle Ax \;:=\; \begin{pmatrix}a_{1,1}x_1+a_{1,2}x_2+\cdots+a_{1,n}x_n\... ...a_{2,n}x_n\\ \vdots\\ a_{m,1}x_1+a_{m,2}x_2+\cdots+a_{m,n}x_n\end{pmatrix}\;. $

Ist $ A = (a_{i,j})_{i\in\{1,\dots,m\},j\in\{1,\dots,n\}}\in K^{m\times n}$ eine Matrix, so heißt

$\displaystyle A^{\mathrm{t}} \; =\; (a_{i,j})_{j\in\{1,\dots,n\},i\in\{1,\dots,m\}} \;\in\; K^{n\times m} $

die zu $ A$ transponierte Matrix. Anschaulich gesprochen geht sie aus $ A$ durch Umwandlung der Spalten in Zeilen hervor. So wird etwa die transponierte Matrix eines Spaltenvektors ein Zeilenvektor.

Zeilenstufenform.

Eine Matrix $ A = (a_{i,j})_{i\in\{1,\dots,m\},j\in\{1,\dots,n\}}\in K^{m\times n}$ heißt in Zeilenstufenform, falls es Spaltenindices $ 1\leq k_1<k_2<\dots<k_r\leq n$ so gibt, daß für $ i=1,\dots,r$ gilt $ a_{i,k_i}=1$ , und sowohl links als auch oberhalb als auch unterhalb von $ a_{i,k_i}=1$ alle Einträge der Matrix gleich 0 sind. Die Zahlen $ k_1,\ldots,k_r$ heißen dann die ausgewählten Spaltenindices. Eine Matrix in Zeilenstufenform sieht so aus:

$\displaystyle \left(\begin{array}{ccccccccccccccc} 0 & \cdots & 0 & 1 & \ast &... ...& \cdots & 0 & 0 & 0 & \cdots & 0 & 0 & 0 & \cdots & 0 \\ \end{array}\right). $

Eine elementare Zeilenumformung einer Matrix $ A$ ist eine der folgenden Operationen.

Der Gaußsche Algorithmus ist ein Verfahren, mit dem eine beliebige Matrix durch elementare Zeilenumformungen in Zeilenstufenform gebracht werden kann. Dabei geht man wie folgt vor.

  1. Man beginne mit der ersten Spalte, welche ein Element $ u\ne 0$ enthält. Deren Spaltennummer sei $ k_1$ .
  2. Durch Zeilenvertauschung bringt man $ u$ in die erste Zeile.
  3. Durch Multiplikation der ersten Zeile mit $ u^{-1}$ steht nun eine $ 1$ in der ersten Zeile der Spalte $ k_1$ .
  4. Durch Addition von geeigneten Vielfachen der ersten Zeile zu den anderen Zeilen werden alle Elemente der Spalte $ k_1$ , die sich nicht in der ersten Zeile befinden, zu 0 .
  5. Man wähle die nächste Spalte, die ein Element $ v\ne 0$ in einer der Zeilen $ 2,\dots,m$ enthält. Deren Spaltennumer sei $ k_2$ .
  6. Durch Zeilenvertauschung bringt man $ v$ in die zweite Zeile.
  7. Durch Multiplikation der zweiten Zeile mit $ v^{-1}$ steht nun eine $ 1$ in der zweiten Zeile der Spalte $ k_2$ .
  8. Durch Addition von geeigneten Vielfachen der zweiten Zeile zu den anderen Zeilen werden alle Elemente der Spalte $ k_2$ , die sich nicht in der zweiten Zeile befinden, zu 0 .
  9. Man setze so fort, bis man die letzte Spalte abgearbeitet hat. Auf diese Weise werden $ r$ Spalten $ k_1,\dots,k_r$ ausgewählt.

Lineare Gleichungssysteme.

Sei $ K$ ein Körper. Seien $ m,n\geq 1$ . Ein lineares Gleichungssystem mit $ m$ Gleichungen in $ n$ Unbekannten ist gegeben durch

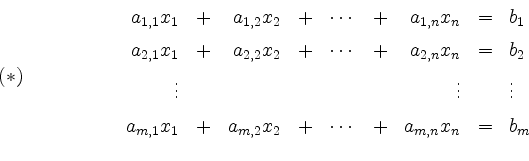
\begin{displaymath} (\ast) \hspace*{2cm} \begin{array}{rcrcrcrcl} a_{1,1}x_1 &+&... ...2 &+& \cdots &+& a_{m,n}x_n &=& b_m\vspace*{2mm}\\ \end{array}\end{displaymath}

mit gegebenen Koeffizienten $ (a_{i,j})_{i\in\{1,\dots,m\},j\in\{1,\dots,n\}}$ und $ (b_j)_{j\in\{1,\dots,m\}}$ aus $ K$ .

Gesucht sind dabei $ x_1,\,\dots,\, x_n$ aus $ K$ so, daß alle obigen Gleichungen erfüllt sind.

Die Variablen $ x_1,\,\dots,\, x_n$ heißen die Unbekannten des Gleichungssystems $ (\ast)$ .

Die Matrix $ A:=(a_{i,j})_{i\in\{1,\dots,m\},j\in\{1,\dots,n\}}$ heißt die Koeffizientenmatrix von $ (\ast)$ .

Die erweiterte Koeffizientenmatrix von $ (\ast)$ ist gegeben durch

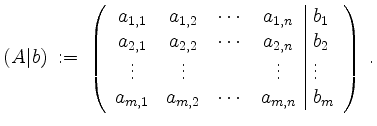
$\displaystyle (A\vert b) \;:=\; \left(\begin{array}{cccc\vert l} a_{1,1} & a_{... ...s & \vdots\\ a_{m,1} & a_{m,2} & \cdots & a_{m,n} & b_m \end{array}\right)\;. $

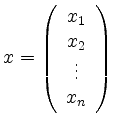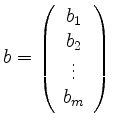Schreiben wir $ x=\left(\begin{array}{c}x_1\\ x_2\\ \vdots\\ x_n\end{array}\right)$ und $ b=\left(\begin{array}{c}b_1\\ b_2\\ \vdots\\ b_m\end{array}\right)$ , so wird $ (\ast)$ zur vektoriellen Gleichung

$\displaystyle (\ast\ast) \hspace*{2cm} Ax \; =\; b\; . $

Die Menge

$\displaystyle L(A,b) \;:=\; \{x\in K^n \;\vert\; Ax = b\} $

der Vektoren $ x$ , die $ (\ast)$ bzw. $ (\ast\ast)$ erfüllen, heißt die Lösungsmenge von $ (\ast)$ bzw. $ (\ast\ast)$ .

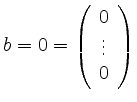Im Falle $ b=0=\left(\begin{array}{c}0\\ \vdots\\ 0\end{array}\right)$ heißt das Gleichungssystem homogen, im anderen Falle inhomogen.

Ist $ x_0\in K^n$ eine partikuläre Lösung, d.h. ein Vektor, für den $ Ax_0 = b$ ist, so gilt für die Lösungsmenge stets

$\displaystyle L(A,b)\;=\; x_0+L(A,0) \;=\; \{x_0+x\vert\; Ax=0\}\; . $

D.h. die Lösungsmenge des inhomogenen Gleichungssystems $ Ax = b$ erhält man, indem man eine gewählte partikuläre Lösung $ x_0$ zur allgemeinen Lösung des zugehörigen homogenen Gleichungssystems $ Ax = 0$ addiert - so denn eine partikuläre Lösung existiert; falls dies nicht der Fall ist, ist das Gleichungssystem unlösbar, d.h. $ L(A,b) = \emptyset$ .

Lösungsverfahren.

Es seien $ A$ und $ b$ wie oben. Um die Lösungsmenge $ L(A,b)$ zu bestimmen, wende man zunächst den Gaußschen Algorithmus auf die erweiterte Matrix $ (A\vert b)$ an, um $ A$ in Zeilenstufenform zu bringen. Die Spalte des Vektors $ b$ wird hierbei mitgeführt. Das so umgeformte System hat dann dieselbe Lösungsmenge wie das ursprüngliche System. Der Einfachheit halber bezeichnen wir die dabei schließlich erhaltene umgeformte Matrix wiederum mit $ (A\vert b)$ .

Seien $ k_1,\ldots,k_r$ die ausgewählten Spaltenindices in $ A$ . Ist $ b_i\ne 0$ für ein $ i>r$ , so ist $ L(A,b) = \emptyset$ , d.h. das Gleichungssystem $ Ax = b$ ist unlösbar. Ansonsten findet man eine partikuläre Lösung $ x_0$ , indem man an die Stellen $ k_1,\ldots,k_r$ von $ x_0$ jeweils die Einträge $ b_1,\ldots,b_r$ von $ b$ einsetzt, und alle anderen Einträge zu Null setzt (positives Einfüllen).

Seien ferner $ k_1',\ldots,k_l'$ die nicht ausgewählten Spaltenindices, $ l = n - r$ . Dann findet man Lösungen $ h_1,\ldots,h_l\in K^n$ des zugehörigen homogenen Systems $ Ax = 0$ , indem man zunächst an der Stelle $ k_i'$ von $ h_i$ eine $ 1$ , an den Stellen aller anderen nicht ausgewählten Spaltenindices eine 0 setzt. Sodann fülle man das jeweilige Negative der ersten $ r$ Einträge der Spalte $ k'_i$ von oben nach unten in die noch freien Stellen von $ h_i$ ein (negatives Einfüllen).

Zur Probe rechne man $ Ax_0 = b$ und $ Ah_i = 0$ für $ i\in\{1,\dots,l\}$ nach, entweder mit der umgeformten, oder - was aufwendiger, aber sicherer ist - mit der ursprünglichen Matrix $ (A\vert b)$ .

Die Lösungsmenge ist dann

$\displaystyle L(A,b) \;=\; \left\{x_0 + \lambda_1 h_1+\cdots+ \lambda_l h_l\vert\; \lambda_1,\ldots,\lambda_l\in K\right\}\;. $

(Autoren: Künzer/Martin/Tentler/Wahrheit)
[Beispiele] [Verweise]
  automatisch erstellt am 11.  8. 2006