Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
Mathematik-Online:

Vektorräume

A B C D E F G H I J K L M N O P Q R S T U V W X Y Z Übersicht

Begriff.

Sei $ K$ ein Körper. Unter einem Vektorraum über $ K$ versteht man eine Menge $ V$ von Vektoren zusammen mit einer Vektoraddition

$\displaystyle V\times V\longrightarrow V,\; (x,y)\mapsto x+y $

und einer Skalarmultiplikation

$\displaystyle K\times V\longrightarrow V,\; (\lambda,x)\mapsto \lambda x $

so, daß die folgenden Axiome erfüllt sind.

Sei $ n\geq 1$ . Das Standardbeispiel eines Vektorraums ist die Menge $ K^n$ aller Spaltenvektoren mit $ n$ Einträgen aus $ K$ , zusammen mit der eintragsweisen Vektoraddition

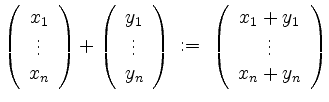
$\displaystyle \left(\begin{array}{c}x_1\\ \vdots\\ x_n\end{array}\right)+\left(... ...ght) \;:=\; \left(\begin{array}{c}x_1+y_1\\ \vdots\\ x_n+y_n\end{array}\right) $

und der eintragsweisen Skalarmutliplikation

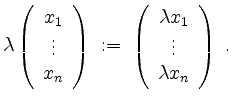
$\displaystyle \lambda \left(\begin{array}{c}x_1\\ \vdots\\ x_n\end{array}\right... ... \left(\begin{array}{c}\lambda x_1\\ \vdots\\ \lambda x_n\end{array}\right)\;. $

Ein weiteres Beispiel ist die Menge $ K[X]$ aller Polynome $ f(X)=\sum_k a_k X^k = \sum_{k\geq 0} a_k X^k$ mit Koeffizienten $ a_k\in K$ , wobei nur endlich viele $ a_k\ne 0$ sind, um eine endliche Summe zu erhalten. Die Menge $ K[X]$ wird zu einem Vektorraum über $ K$ mit der Vektoraddition

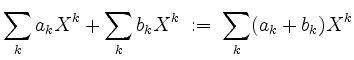
$\displaystyle \sum_k a_k X^k + \sum_k b_k X^k \;:=\; \sum_k (a_k+b_k) X^k $

und der Skalarmultiplikation

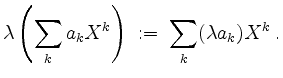
$\displaystyle \lambda \left(\sum_k a_k X^k\right) \;:=\; \sum_k (\lambda a_k) X^k\;. $

Unterräume.

Sei $ V$ ein Vektorraum über dem Körper $ K$ . Unter einem Unterraum von $ V$ versteht man eine Teilmege $ U\subseteq V$ von $ V$ mit den folgenden Eigenschaften.

Diese Bedingungen sind gleichbedeutend damit, daß $ U$ mit der in $ V$ definierten Vektoraddition und Skalarmultiplikation selbst ein Vektorraum ist.

Die Teilmengen $ \{0\}$ und $ V$ sind stets Unterräume eines Vektorraums $ V$ .

Der Durchschnitt von Unterräumen von $ V$ ist wieder ein Unterraum von $ V$ .

Basen.

Sei $ V$ ein fester Vektorraum über dem Körper $ K$ . Sei $ (x_1,\ldots,x_n)$ ein Tupel von Vektoren $ x_1,\,\ldots,\, x_n\,\in\, V$ .

Unter einer Linearkombination von $ (x_1,\ldots,x_n)$ über $ K$ versteht man einen Vektor der Form

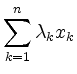
$\displaystyle \sum_{k=1}^n \lambda_k x_k $

mit $ \lambda_1,\ldots,\lambda_n\in K$ . Diese Linearkombination heißt trival, falls alle $ \lambda_k=0$ sind.

Die Menge

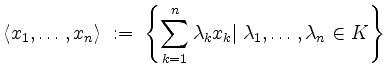
$\displaystyle \langle x_1,\ldots,x_n\rangle \;:=\; \left\{\sum_{k=1}^n\lambda_k x_k\vert\; \lambda_1,\ldots,\lambda_n\in K\right\} $

der Linearkombinationen von $ (x_1,\ldots,x_n)$ wird als das Erzeugnis von $ (x_1,\ldots,x_n)$ bezeichnet. Es handelt sich dabei um einen Unterraum von $ V$ .

Das Tupel $ (x_1,\ldots,x_n)$ heißt linear abhängig, falls es eine nicht-triviale Linearkombination

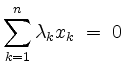
$\displaystyle \sum_{k=1}^n \lambda_k x_k \; =\; 0 $

gibt. Anderenfalls heißt das Tupel $ (x_1,\ldots,x_n)$ linear unabhängig.

Das Tupel $ (x_1,\ldots,x_n)$ ist also linear unabhängig genau dann, wenn 0 sich nur als triviale Linearkombination von $ (x_1,\ldots,x_n)$ schreiben läßt.

Das Tupel $ (x_1,\ldots,x_n)$ heißt erzeugend in $ V$ oder ein Erzeugendensystem von $ V$ , falls sich jeder Vektor in $ V$ als Linearkombination von $ (x_1,\ldots,x_n)$ schreiben läßt, d.h. falls

$\displaystyle \langle x_1,\ldots,x_n\rangle\; =\; V \; . $

Das Tupel $ (x_1,\ldots,x_n)$ heißt eine Basis von $ V$ , falls es linear unabhängig und erzeugend in $ V$ ist. Dies ist gleichbedeutend damit, daß sich jeder Vektor in $ V$ in eindeutiger Weise als Linearkombination von $ (x_1,\ldots,x_n)$ darstellen läßt.

Eine Basis des Vektorraums $ K^n$ ist zum Beispiel die Standardbasis, bestehend aus den $ n$ Einheitsvektoren

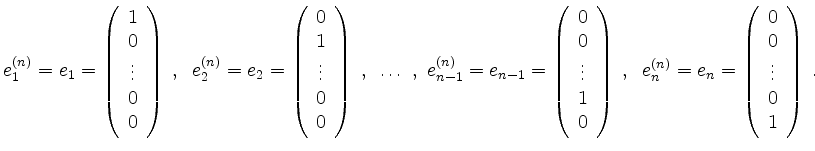
$\displaystyle e_1^{(n)}=e_1=\left(\begin{array}{c}1\\ 0\\ \vdots\\ 0\\ 0\end{ar... ...n^{(n)}=e_n=\left(\begin{array}{c}0\\ 0\\ \vdots\\ 0\\ 1\end{array}\right)\; . $

Ist $ (x_1,\ldots,x_n)$ eine Basis von $ V$ , so ist die Anzahl der Vektoren in jeder Basis von $ V$ gleich $ n$ und wird als die Dimension von $ V$ bezeichnet, in Zeichen $ \dim V = n$ . In diesem Falle heißt der Vektorraum $ V$ endlichdimensional.

Der Vektorraum $ \{0\}$ besitzt die Basis $ ()$ , das leere Tupel. Seine Dimension ist $ \dim\{0\}=0$ .

Besitzt der Vektorraum $ V$ keine (endliche) Basis, so schreiben wir $ \dim V=\infty$ .

Ist $ U$ ein Unterraum von $ V$ , so gilt stets $ \dim U\leq \dim V$ . Es gilt $ \dim U=\dim V$ genau dann, wenn $ U=V$ .

Basisauswahlsatz.

Besitzt $ V$ ein Erzeugendensystem $ (x_1,\ldots,x_m)$ , so läßt sich aus dem Tupel $ (x_1,\ldots,x_m)$ durch eventuelles Weglassen von Vektoren eine Basis von $ V$ auswählen. Insbesondere ist $ \dim V\leq m$ .

Ein erzeugendes Tupel in $ V$ der Länge $ \dim V$ ist stets eine Basis.

Praktisches Verfahren zur Auswahl einer Basis.

Sei $ U$ ein Unterraum von $ K^n$ mit Erzeugendensystem $ (x_1,\ldots,x_m)$ . Um aus diesem Tupel eine Basis von $ U$ auszuwählen, schreibt man die Vektoren $ x_1,\dots,x_m$ als Spalten in eine Matrix und bringt diese auf Zeilenstufenform. Seien $ k_1,\dots,k_r$ die Nummern der ausgewählten Spalten. Dann ist $ (x_{k_1},\dots,x_{k_r})$ eine Basis von $ U$ .

Basisergänzungssatz.

Ist $ (x_1,\ldots,x_l)$ ein linear unabhängiges Tupel in einem Unterraum $ U$ von $ V$ , so läßt es sich durch eventuelles Hinzufügen von Vektoren zu einer Basis von $ V$ ergänzen. Insbesondere ist $ \dim U\geq l$ .

Ein linear unabhängiges Tupel in $ V$ der Länge $ \dim V < \infty$ ist stets eine Basis.

Praktisches Verfahren zur Basisergänzung.

Sei $ (x_1,\dots,x_l)$ ein linear unabhängiges Tupel von Vektoren in $ U = \langle x_{l+1},\dots,x_{l+m}\rangle$ . Schreibe $ (x_1,\dots,x_l,x_{l+1},\dots,x_{l+m})$ in die Spalten einer Matrix und bringe diese in Zeilenstufenform. Sind $ k_1$ , ..., $ k_{l+s}$ ihre ausgewählten Spalten, so ist $ k_i = i$ für $ 1\leq i\leq l$ und $ (x_{k_1},\dots,x_{k_{l+s}})$ eine Ergänzung von $ (x_1,\dots,x_l)$ zu einer Basis von $ U$ .

Direkte Summe.

Seien $ U_1,\ldots, U_m$ Unterräume des Vektorraums $ V$ .

Die Summe der Unterräume $ U_1,\ldots, U_m$ ist definiert als

$\displaystyle U_1+\cdots+U_m \;:=\; \{x_1+\cdots+ x_m\vert\; x_1\in U_1,\ldots,x_m\in U_m\}\;. $

Die Summe von Unterräumen von $ V$ ist wieder ein Unterraum von $ V$ .

Diese Summe heißt direkt, in Zeichen

$\displaystyle U_1\oplus\cdots\oplus U_m\; , $

falls aus $ x_1+\cdots+x_m=0$ mit $ x_1\in U_1,\,\ldots,\,x_m\,\in\, U_m$ stets $ x_1 = \ldots = x_m = 0$ folgt. Diese Bedingung ist gleichbedeutend damit, daß für jeden Vektor $ x_1+\ldots+x_m$ aus $ U_1+\cdots+U_m$ die Summanden $ x_1\in U_1,\,\ldots,\,x_m\,\in\, U_m$ eindeutig bestimmt sind.

Im Falle zweier Unterräume $ U_1$ , $ U_2$ von $ V$ ist die Summe $ U_1+U_2$ direkt genau dann, wenn $ U_1\cap U_2=\{0\}$ .

Sind Basen $ (x_1^{(k)},\ldots,x_{n_k}^{(k)})$ von $ U_k$ gegeben für $ 1\leq k\leq m$ , so ist die Summe $ U_1+\cdots+U_m$ genau dann direkt, wenn das zusammengesetzte Tupel

$\displaystyle (x_1^{(1)},\ldots,x_{n_1}^{(1)},x_1^{(2)},\ldots,x_{n_2}^{(2)},\dots,x_1^{(m)},\ldots,x_{n_m}^{(m)}) $

linear unabhängig ist. In diesem Falle ist dieses Tupel eine Basis von $ U_1\oplus\cdots\oplus U_m$ .

Dimensionsformel.

Seien $ U_1,U_2$ Unterräume des Vektorraums $ V$ . Dann gilt die Dimensionsformel

$\displaystyle \dim(U_1+U_2) \;=\; \dim U_1+\dim U_2-\dim (U_1\cap U_2)\;. $

Zassenhaus-Algorithmus.

Der Zassenhaus-Algorithmus ist ein praktisches Verfahren zur Bestimmung von Basen von $ U_1+U_2$ und $ U_1\cap U_2$ , wenn $ U_1,U_2$ Unterräume von $ K^n$ sind und Erzeugendensysteme jeweils gegeben sind.

Sei etwa $ U_1=\langle x_1,\dots,x_k\rangle$ und $ U_2=\langle y_1,\dots,y_l\rangle$ . Seien $ x_1^\mathrm{t},\dots,x_k^\mathrm{t}$ und $ y_1^\mathrm{t},\dots,y_l^\mathrm{t}$ die entsprechenden Zeilenvektoren. Man betrachte nun die folgende Matrix und bringe sie auf Zeilenstufenform:

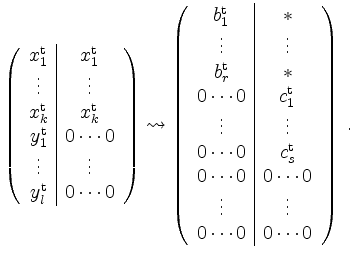
$\displaystyle \left(\begin{array}{c\vert c} x_1^\mathrm{t} & x_1^\mathrm{t} \\ ... ...dots 0 \\ \vdots & \vdots \\ 0\cdots 0 & 0\cdots 0 \\ \end{array}\right)\;. $

Dabei seien die Zeilen $ b_1^\mathrm{t},\dots,b_r^\mathrm{t}$ und $ c_1^\mathrm{t},\dots,c_s^\mathrm{t}$ jeweils ungleich 0 .

Dann ist $ (b_1,\dots,b_r)$ eine Basis von von $ U_1+U_2$ , und $ (c_1,\dots,c_s)$ ist eine Basis von $ U_1\cap U_2$ .

(Autoren: Künzer/Martin/Tentler/Wahrheit)

siehe auch:

[Beispiele]
  automatisch erstellt am 16.  2. 2011