Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
Mathematik-Online:

Lineare Abbildungen und Darstellungsmatrizen

A B C D E F G H I J K L M N O P Q R S T U V W X Y Z Übersicht

Seien $ V$ und $ W$ Vektorräume über dem Körper $ K$ .

Begriff.

Eine Abbildung $ f:V\longrightarrow W$ heißt linear, falls

$\displaystyle f(\lambda x + \mu y) \;=\; \lambda f(x) + \mu f(y) $

für alle $ x,y\in V$ und alle $ \lambda,\mu\in K$ .

Ist $ V=K^n$ und $ W=K^m$ , und ist $ A\in K^{m\times n}$ eine Matrix, so ist zum Beispiel die Abbildung

$\displaystyle K^n\longrightarrow K^m,\; x\mapsto Ax $

linear.

Eine lineare Abbildung $ V\longrightarrow V$ heißt auch Endomorphismus von $ V$ .

Die Verkettung linearer Abbildungen ist wieder eine lineare Abbildung.

Ist $ f:V\longrightarrow W$ eine lineare Abbildung, so ist

$\displaystyle \operatorname{Kern }f \; :=\; \{x\in V\vert\; f(x)=0\} \;=\; f^{-1}(\{0\}) $

ein Unterraum von $ V$ , genannt der Kern von $ f$ . Ferner ist

$\displaystyle \operatorname{Bild } f \; :=\; \{f(x)\; \vert\; x\in V\} \;=\; f(V) $

ein Unterraum von $ W$ , genannt das Bild von $ f$ .

Die lineare Abbildung $ f$ ist injektiv genau dann, wenn $ \operatorname{Kern }f=\{0\}$ .

Ist die lineare Abbildung $ f:V\longrightarrow W$ bijektiv, so ist auch die Umkehrabbildung $ f^{-1}:W\longrightarrow V$ wieder eine lineare Abbildung.

Eine bijektive lineare Abbildung $ f:V\to W$ heißt auch Isomorphismus. Ein isomorpher Endomorphismus heißt auch Automorphismus.

So etwa ist die identische Abbildung $ V\longrightarrow V,\ x\mapsto x$ ein Isomorphismus.

Kriterien.

Sei $ f:V\to W$ eine lineare Abbildung. Sei $ (x_1,\dots,x_n)$ eine Basis von $ V$ .

Die lineare Abbildung $ f$ ist injektiv genau dann, wenn $ (f(x_1),\dots,f(x_n))$ linear unabhängig in $ W$ ist.

Die lineare Abbildung $ f$ ist surjektiv genau dann, wenn $ (f(x_1),\dots,f(x_n))$ erzeugend in $ W$ ist.

Die lineare Abbildung $ f$ ist bijektiv genau dann, wenn $ (f(x_1),\dots,f(x_n))$ eine Basis von $ W$ ist.

Dimensionsformel.

Sei $ f:V\longrightarrow W$ eine lineare Abbildung. Dann gilt die Dimensionsformel

$\displaystyle \dim V \;=\; \dim\operatorname{Kern }f + \dim\operatorname{Bild } f \;. $

Matrixmultiplikation.

Seien $ A=(a_{i,j})_{i,j}\in K^{l\times m}$ und $ B=(b_{j,k})_{j,k}\in K^{m\times n}$ Matrizen. Das Matrixprodukt von $ A$ und $ B$ ist definiert als

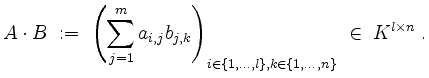
$\displaystyle A\cdot B \;:=\; \left(\sum_{j=1}^m a_{i,j}b_{j,k}\right)_{i\in\{1,\dots,l\},k\in\{1,\dots,n\}} \;\in\; K^{l\times n}\;. $

Der Eintrag an der Position $ (i,j)$ von $ A\cdot B$ berechnet sich also aus der $ i$ -ten Zeile von $ A$ und der $ j$ -ten Spalte von $ B$ .

Ist $ A\in K^{m\times m}$ , so setzen wir $ A^0:=\mathrm{E}_m$ , $ A^1:=A$ , $ A^2:=A\cdot A$ , ..., $ A^k:=A\cdot A^{k-1}$ .

Vorsicht! Es gilt i.a. $ A\cdot B \ne B\cdot A$ für $ A, B\in K^{m\times m}$ .

Darstellungsmatrix.

Sei $ f:V\longrightarrow W$ eine lineare Abbildung. Sei $ \underline{x}=(x_1,\dots,x_n)$ eine Basis von $ V$ , und sei $ \underline{y}=(y_1,\dots,y_m)$ eine Basis von $ W$ .

Dann gibt es eindeutig bestimmte Koeffizienten $ (a_{i,j})_{i\in\{1,\dots,m\}, j\in\{1,\dots,n\}}$ in $ K$ so, daß

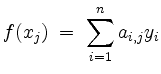
$\displaystyle f(x_j) \;=\; \sum_{i=1}^n a_{i,j} y_i $

für alle $ j\in\{1,\dots,n\}$ . Die zugehörige Matrix

$\displaystyle \mathrm{M}(f)_{\underline{y},\underline{x}} \;:=\; (a_{i,j})_{i\in\{1,\dots,m\}, j\in\{1,\dots,n\}} \;\in\; K^{m\times n} $

heißt die Darstellungsmatrix von $ f$ bezüglich der Basen $ \underline{x}$ und $ \underline{y}$ .

Kurz, die Spalten der Darstellungsmatrix sind die Koeffizienten der Bilder der Basisvektoren von $ V$ bezüglich der Basis von $ W$ .

Ist $ Y$ ein weiterer Vektorraum über $ K$ mit Basis $ \underline{z}=(z_1,\dots,z_l)$ , und ist $ g:W\longrightarrow Y$ eine lineare Abbildung, so ist

$\displaystyle \mathrm{M}(g\circ f)_{\underline{z},\underline{x}} \;=\; \mathrm{... ...derline{z},\underline{y}} \cdot \mathrm{M}(f)_{\underline{y},\underline{x}}\;, $

d.h. die Darstellungsmatrix der Verkettung ist gleich dem Matrixprodukt der Darstellungsmatrizen.

Ist $ V=K^n$ , $ W=K^m$ , sind $ \underline{e}^{(n)}$ bzw. $ \underline{e}^{(m)}$ die Standardbasen des $ K^n$ bzw. $ K^m$ , und ist $ f:K^n\longrightarrow K^m$ , $ x\mapsto Ax$ , wobei $ A\in K^{m\times n}$ , so ist

$\displaystyle \mathrm{M}(f)_{\underline{e}^{(m)},\underline{e}^{(n)}} \;=\; A \;, $

d.h. die Multiplikation mit $ A$ hat die Darstellungsmatrix $ A$ bezüglich der Standardbasen. Wir schreiben in diesem Falle auch

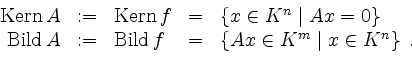
\begin{displaymath} \begin{array}{rclcl} \operatorname{Kern }A & := & \operatorn... ...t\{ Ax \in K^m \;\vert\; x \in K^n \right\}\; . \\ \end{array}\end{displaymath}

Rang einer Matrix.

Sei $ A=(a_{i,j})_{i,j}\in K^{m\times n}$ eine Matrix, und seien $ a_{\ast,1},\dots,a_{\ast,n}\in K^m$ die Spaltenvektoren von $ A$ . Dann ist der Rang von $ A$ definiert durch

$\displaystyle \operatorname{Rang } A \;:=\; \dim\langle a_{\ast,1},\ldots,a_{\ast,n}\rangle \;. $

Es ist

$\displaystyle \operatorname{Rang} A \;=\; \operatorname{Rang} A^\mathrm{t} \;, $

d.h.

$\displaystyle \operatorname{Rang} A \; =\; \dim\langle a_{\ast,1},\ldots,a_{\as... ...=\; \dim\langle a_{1,\ast}^\mathrm{t},\ldots,a_{m,\ast}^\mathrm{t}\rangle \; . $

Zur Berechnung des Rangs bringe man die Matrix $ A$ in Zeilenstufenform. Der Rang ist dann gleich der Anzahl der Nichtnullzeilen in der Zeilenstufenform.

Seien $ A\in K^{m\times n}$ und $ B\in K^{n\times r}$ Matrizen. Dann gilt

$\displaystyle \operatorname{Rang}(A\cdot B) \;\leq\; \min\{\operatorname{Rang} A,\operatorname{Rang} B\}\;. $

Ist $ f:V\longrightarrow W$ eine lineare Abbildung, und sind $ \underline{x}$ bzw. $ \underline{y}$ Basen von $ V$ bzw. $ W$ , so gilt

$\displaystyle \dim\operatorname{Bild} f \;=\; \operatorname{Rang } \mathrm{M}(f)_{\underline{y},\underline{x}}\;. $

Invertierbarkeit.

Sei $ A\in K^{n\times n}$ eine quadratische Matrix, d.h. ihre Spaltenzahl ist gleich ihrer Zeilenzahl.

$ A$ heißt invertierbar oder regulär, falls es eine Matrix $ B\in K^{n\times n}$ gibt so, daß

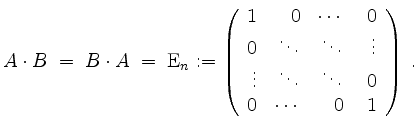
$\displaystyle A\cdot B \;=\; B\cdot A \;=\; \mathrm{E}_n:=\left(\begin{array}{r... ...\\ \vdots & \ddots & \ddots & \ 0\\ 0 & \cdots & 0 & 1 \end{array}\right)\;. $

In diesem Falle ist die Matrix $ B$ eindeutig bestimmt. Sie wird mit $ A^{-1}$ bezeichnet und heißt die Inverse von A.

Die Matrix $ A$ heißt singulär, falls sie nicht regulär ist.

Für eine quadratische Matrix $ A\in K^{n\times n}$ sind folgende Aussagen äquivalent.

Seien $ V$ und $ W$ Vektorräume derselben Dimension $ n$ , seien $ \underline{x}$ bzw. $ \underline{y}$ Basen von $ V$ bzw. $ W$ , und sei $ f:V\longrightarrow W$ eine lineare Abbildung. Dann sind folgende Aussagen äquivalent.

In diesem Falle ist

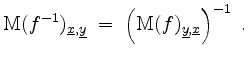
$\displaystyle \mathrm{M}(f^{-1})_{\underline{x},\underline{y}} \;=\; \left(\mathrm{M}(f)_{\underline{y},\underline{x}}\right)^{-1} \;. $

Berechnung der Inversen.

Sei $ A\in K^{n\times n}$ eine quadratische Matrix.

Um $ A$ auf Invertierbarkeit zu überprüfen und gegebenenfalls die Inverse von $ A$ zu berechnen, wende man den Gaußschen Algorithmus auf die folgende Matrix an.

$\displaystyle (A\vert\mathrm{E}_n) \leadsto (\mathrm{E}_n\vert A^{-1}) \;. $

Hierbei kann $ A$ in die Einheitsmatrix überführt werden genau dann, wenn $ A$ invertierbar ist. In diesem Falle entsteht in der rechten Hälfte aus $ \mathrm{E}_n$ die Inverse $ A^{-1}$ von $ A$ .

(Autoren: Künzer/Martin/Tentler/Wahrheit)
[Beispiele] [Verweise]
  automatisch erstellt am 22.  8. 2006