Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
Mathematik-Online:

Die Jordanform

A B C D E F G H I J K L M N O P Q R S T U V W X Y Z Übersicht

Eigenräume und Haupträume.

Sei $ A=(a_{i,j})_{i,j}\in\mathbb{C}^{n\times n}$ . Ein Eigenwert von $ A$ ist eine komplexe Zahl $ \lambda\in\mathbb{C}$ derart, daß es einen Vektor $ x\in\mathbb{C}^n\setminus\{ 0\}$ gibt mit

$\displaystyle Ax \;=\; \lambda x\;. $

Jeder solche Vektor heißt Eigenvektor von $ A$ zum Eigenwert $ \lambda$ .

Das charakteristische Polynom von $ A$ ist gegeben durch

$\displaystyle \chi_A(X) \;:=\; \det(X\mathrm{E}-A) \;=\; X^n+h_{n-1}X^{n-1}+\cdots+h_1X+h_0\in \mathbb{C}[X]\;. $

Stets läßt sich $ \chi_A(X)$ faktorisieren in

$\displaystyle \chi_A(X) \;=\; (X-\lambda_1)^{m_1}\cdots(X-\lambda_r)^{m_r}\;, $

wobei $ \lambda_1,\ldots,\lambda_r\in\mathbb{C}$ die paarweise verschiedenen Eigenwerte von $ A$ sind, und $ m_1,\ldots,m_r\geq 1$ .

Der Exponent $ m_i$ heißt algebraische Vielfachheit des Eigenwerts $ \lambda_i$ .

Es ist

$\displaystyle h_{n-1} \;=\; -(m_1\lambda_1+\cdots+m_r\lambda_r) = -\mathrm{Spur} A \;=\; -(a_{1,1}+\cdots+a_{n,n})\; , $

und

$\displaystyle h_0 \;=\; (-1)^n\lambda_1^{m_1}\cdots\lambda_r^{m_r} \;=\; (-1)^n\det A \;. $

Der Eigenraum zum Eigenwert $ \lambda_i$ von $ A$ ist gegeben durch

$\displaystyle \mathrm{E}_A(\lambda_i) \;:=\; \operatorname{Kern}(A-\lambda_i\mathrm{E}) \;=\; \{x\in\mathbb{C}^n \;\vert\; Ax=\lambda_i x\}\;. $

Seine Dimension heißt geometrische Vielfachheit des Eigenwerts $ \lambda_i$ .

Der Hauptraum zum Eigenwert $ \lambda_i$ von $ A$ ist gegeben durch

$\displaystyle \mathrm{H}_A(\lambda_i) \;:=\; \operatorname{Kern}((A-\lambda_i\mathrm{E})^{m_i}) \;. $

Seine Dimension ist gleich der algebraischen Vielfachheit von $ \lambda_i$ .

Insbesondere ist $ 1 \;\leq\;$   (geometrische Vielfachheit von $ \lambda_i$ )$ \;\leq\;$   (algebraische Vielfachheit von $ \lambda_i$ )$ =m_i$ .

Die Zerlegung

$\displaystyle \mathbb{C}^n \;=\; \mathrm{H}_A(\lambda_1) \oplus\cdots\oplus \mathrm{H}_A(\lambda_r) $

heißt die Hauptraumzerlegung von $ \mathbb{C}^n$ bezüglich $ A$ .

Die Jordanform.

Sei $ \lambda\in\mathbb{C}$ und $ k\geq 1$ . Die Matrix

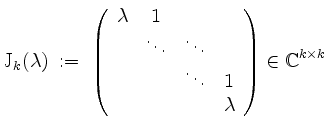
$\displaystyle \mathrm{J}_k(\lambda) \;:=\; \left(\begin{array}{cccc} \lambda &... ... & & \ddots & 1 \\ & & & \lambda \end{array}\right)\in\mathbb{C}^{k\times k} $

heißt Jordanblock der Größe (oder Kantenlänge) $ k$ zum Eigenwert $ \lambda$ . Dabei seien nicht erwähnte Einträge gleich 0 .

Eine Matrix $ J\in\mathbb{C}^{n\times n}$ heißt in Jordanform, falls sie eine aus Jordanblöcken bestehende Blockdiagonalmatrix ist.

Sei $ A\in\mathbb{C}^{n\times n}$ gegeben. Wir wollen eine reguläre Matrix $ S\in\mathbb{C}^{n\times n}$ so finden, daß $ S^{-1}AS$ in Jordanform ist.

Algorithmus.

Ist $ \underline{y}=(y_1,\ldots,y_l)$ ein Tupel von Vektoren im $ \mathbb{C}^n$ , und ist $ C\in\mathbb{C}^{n\times n}$ eine Matrix, so sei

$\displaystyle C\underline{y} \;:=\; (Cy_1,\ldots,Cy_l)\;. $

Der nun folgende Algorithmus liefert eine Transformationsmatrix $ S$ sowie eine Jordanform $ J$ der Matrix $ A$ .

(1)
Berechne das charakteristische Polynom in der Form $ \chi_A(X) \;=\; (X-\lambda_1)^{m_1}\cdots(X-\lambda_r)^{m_r}$ .
(2)
Führe die Schritte (3), (4) und (5) für jedes $ i\in\{1,\ldots,r\}$ durch.
(3)
Sei $ C:=A-\lambda_iE$ . Berechne ein Basistupel $ \underline{y}_1$ von $ \operatorname{Kern}(C^1)$ , ergänze dieses zu einem Basistupel $ (\underline{y}_1,\underline{y}_2)$ von $ \operatorname{Kern}(C^2)$ , und so fort, bis die ergänzte Basis $ (\underline{y}_1,\ldots,\underline{y}_l)$ die Länge $ m_i$ hat. Dies ist dann eine Basis von $ \mathrm{H}_A(\lambda_i)$ .

Wir können dies in einem Tableau eintragen.

Stufe $ 1$ $ \underline{y}_1=$ Basis von $ \operatorname{Kern } C$
Stufe $ 2$ $ \underline{y}_2=$ Basisergänzung zu $ \operatorname{Kern}(C^2)$
$ \vdots$ $ \vdots$
Stufe $ l-1$ $ \underline{y}_{l-1}=$ Basisergänzung zu $ \operatorname{Kern}(C^{l-1})$
Stufe $ l$ $ \underline{y}_l=$ Basisergänzung zu $ \operatorname{Kern}(C^l)$

(4)
Dieser Schritt unterteilt sich in Teilschritte $ (l)$ , $ (l-1)$ , ..., $ (1)$ , welche man auch als Stufen bezeichnet.

$ (l)$
Sei $ \underline{x}_l:=\underline{y}_l$ das zuletzt hinzugefügte Tupel.
$ (l-1)$
Ergänze $ (\underline{y}_1,\ldots,\underline{y}_{l-2},C\underline{x}_l)$ durch eine (möglicherweise leere) Auswahl $ \underline{x}_{l-1}$ aus $ \underline{y}_{l-1}$ zu einer Basis $ (\underline{y}_1,\ldots,\underline{y}_{l-2},C\underline{x}_l,\underline{x}_{l-1})$ von $ \operatorname{Kern}(C^{l-1})$ .
$ (l-2)$
Ergänze $ (\underline{y}_1,\ldots,\underline{y}_{l-3},C^2\underline{x}_l,C\underline{x}_{l-1})$ durch eine (möglicherweise leere) Auswahl $ \underline{x}_{l-2}$ aus $ \underline{y}_{l-2}$ zu einer Basis $ (\underline{y}_1,\ldots,\underline{y}_{l-3},C^2\underline{x}_l,C\underline{x}_{l-1},\underline{x}_{l-2})$ von $ \operatorname{Kern}(C^{l-2})$ .
$ (\vdots)$
$ (1)$
Ergänze $ (C^{l-1}\underline{x}_l,C^{l-2}\underline{x}_{l-1},\ldots,C\underline{x}_2)$ durch eine (möglicherweise leere) Auswahl $ \underline{x}_1$ aus $ \underline{y}_1$ zu einer Basis $ (C^{l-1}\underline{x}_l,C^{l-2}\underline{x}_{l-1},\ldots,C\underline{x}_2,\underline{x}_1)$ von $ \operatorname{Kern}(C^1)$ .

Im Tableau trägt man dabei für $ k=l-1,l-2,\ldots,2,1$ jeweils das $ C$ -fache der Vektoren einer Stufe $ k+1$ in die Stufe $ k$ ein, und bildet dann das Tupel $ \underline{x}_k$ aus dem Tupel $ \underline{y}_k$ durch Streichen von Vektoren derart, daß schließlich in der Stufe $ k$ wieder eine Basisergänzung zu $ \operatorname{Kern}(C^k)$ steht. Das Tableau sieht dann wie folgt aus.

Stufe $ 1$ $ \underline{x}_1$ , $ C\underline{x}_2,\ldots,C^{l-1}\underline{x}_l$
Stufe $ 2$ $ \underline{x}_2$ , $ C\underline{x}_3,\ldots,C^{l-2}\underline{x}_l$
$ \vdots$ $ \vdots$
Stufe $ l-2$ $ \underline{x}_{l-2}$ , $ C\underline{x}_{l-1}$ , $ C^2\underline{x}_l$
Stufe $ l-1$ $ \underline{x}_{l-1}$ , $ C\underline{x}_l$
Stufe $ l$ $ \underline{x}_l:=\underline{y}_l$

(5)
Für $ j\in\{1,\dots,l\}$ schreiben wir nun ausführlich $ \underline{x}_j=(x_{j,1},\ldots,x_{j,k_j})$ , bestehend aus Vektoren $ x_{j,t}$ . Sortiere die erhaltenen Vektoren zu Ketten

$\displaystyle \mathrm{Kette}(x_{j,t}) \;:=\; (C^{j-1}x_{j,t},C^{j-2}x_{j,t},\dots,Cx_{j,t},x_{j,t}) $

und trage das Tupel

$\displaystyle (\mathrm{Kette}(x_{l,1}),\dots,\mathrm{Kette}(x_{l,k_l}),\mathrm{... ..._{l-1,k_{l-1}}),\dots,\mathrm{Kette}(x_{1,1}),\dots,\mathrm{Kette}(x_{1,k_1})) $

als Spalten in die zu bildende Matrix $ S$ ein.

Diese Ketten kann man im Tableau direkt ablesen, wenn man in Schritt (4) jeden Vektor $ x$ der Stufe $ k$ mit seinem Bild $ Cx$ in der Stufe $ k-1$ verbindet, für alle $ k$ . Auf diese Art gewinnt man Ketten, die alle in Stufe $ 1$ beginnen. Die Vektoren jeder Kette trägt man dann in die Matrix $ S$ ein, jeweils beginnendend mit dem Vektor in Stufe $ 1$ .

Trage schließlich in die zu bildende Matrix $ J$ die Jordanblöcke

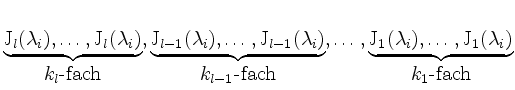
$\displaystyle \underbrace{\mathrm{J}_l(\lambda_i),\dots,\mathrm{J}_l(\lambda_i)... ...ace{\mathrm{J}_1(\lambda_i),\dots,\mathrm{J}_1(\lambda_i)}_{\mbox{$k_1$-fach}} $

in dieser Reihenfolge auf der Hauptdiagonalen ein.

Hat man dies für alle $ i=1,\ldots,r$ durchgeführt, so haben $ S$ und $ J$ am Ende die gewünschten Eigenschaften, d.h. es gilt $ S^{-1}AS=J$ und $ J$ ist in Jordanform.

Erläuterungen zu diesem Algorithmus.

zu (3)
Zur Berechnung von $ \operatorname{Kern}(C^1)$ bringen wir $ C$ auf Zeilenstufenform und streichen Nullzeilen. Die entstandene Matrix heiße $ Z_1$ .
Zur Berechnung von $ \operatorname{Kern}(C^2) = \operatorname{Kern}(Z_1\cdot C)$ bringen wir $ Z_1\cdot C$ auf Zeilenstufenform und streichen Nullzeilen. Die entstandene Matrix heiße $ Z_2$ .
Zur Berechnung von $ \operatorname{Kern}(C^3) = \operatorname{Kern}(Z_2\cdot C)$ bringen wir $ Z_2\cdot C$ auf Zeilenstufenform und streichen Nullzeilen. Die entstandene Matrix heiße $ Z_3$ .
Und so fort.

zu (3)
Solange $ \dim\operatorname{Kern}(C^j) < m_i$ ist, ist auch $ \dim\operatorname{Kern}(C^j) < \dim\operatorname{Kern}(C^{j+1})$ . D.h. in diesem Falle muß $ \operatorname{Rang } Z_j > \operatorname{Rang } Z_{j+1}$ sein. Ist das nicht der Fall, liegt ein Rechenfehler vor.
zu (4)
In Schritt $ (4)$ für $ l\geq j\geq 1$ wählen wir ein geeignet aussehendes Tupel der richtigen Länge für die Basisergänzung aus und testen das ergänzte Tupel auf lineare Unabhängigkeit. Oder aber, sicherer, wir berechnen die Zeilenstufenform, die uns sagt, welche Vektoren ausgewählt werden können.
zu (4, 5)
Ist das ausgewählte Tupel $ \underline{x}_j$ leer, so ist $ k_j=0$ .
als Probe
Zur Probe verifizieren wir, daß $ SJ=AS$ gilt, sowie, daß $ S$ regulär ist.

Die Jordanform einer Matrix $ A$ ist bis auf Reihenfolge der Jordanblöcke eindeutig bestimmt. Die Matrix $ S$ ist hingegen nicht eindeutig bestimmt.

Minimalpolynom.

Sei

$\displaystyle f(X) \;=\; \sum_{i=0}^d c_i X^i\;\in\;\mathbb{C}[X] $

ein Polynom. Setze

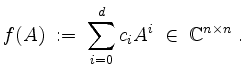
$\displaystyle f(A) \;:=\; \sum_{i=0}^d c_i A^i\;\in\;\mathbb{C}^{n\times n}\;. $

Man sagt, das Polynom $ f(X)$ annulliert die Matrix $ A$ , falls $ f(A)=0$ .

Das normierte Polynom kleinsten Grades, welches $ A$ annulliert, heißt das Minimalpolynom von $ A$ und wird mit $ \mu_A(X)$ bezeichnet. Jedes Polynom, welches $ A$ annulliert, ist ein Vielfaches von $ \mu_A(X)$ .

Das Minimalpolynom von $ A$ ergibt sich zu

$\displaystyle \mu_A(X) \;=\; (X-\lambda_1)^{l_1}(X-\lambda_2)^{l_2}\cdots(X-\lambda_r)^{l_r}\;, $

wobei $ l_i$ die maximale Kantenlänge eines Jordanblocks zum Eigenwert $ \lambda_i$ in der Jordanform von $ A$ ist.

Insbesondere ist die Nullstellenmenge von $ \mu_A(X)$ gleich der Nullstellenmenge von $ \chi_A(X)$ , nämlich gleich der Menge der Eigenwerte $ \{\lambda_1,\dots,\lambda_r\}$ von $ A$ .

Berechnet man das Minimalpolynom von $ A$ direkt, in der Regel unter Zuhilfenahme von iteriert mit $ A$ multiplizierten Vektoren und entsprechenden linearen Gleichungssystemen, so kann man auch das Minimalpolynom zur Berechnung der Eigenwerte von $ A$ heranziehen. Wir wollen dies hier nicht weiter verfolgen.

Der Satz von Cayley-Hamilton besagt, daß $ \chi_A(A)=0$ ist. Insbesondere ist $ \chi_A(X)$ ein Vielfaches von $ \mu_A(X)$ . Dies spiegelt sich in den Exponenten wieder, es ist $ l_i\leq m_i$ .

Diagonalisierbarkeit.

Die geometrische Vielfachheit eines Eigenwertes von $ A$ ist gleich der Anzahl der Jordanblöcke zu diesem Eigenwert. Seine algebraische Vielfachheit ist gleich der Summe der Kantenlängen der Jordanblöcke zu diesem Eigenwert, d.h. seine Vielfachheit auf der Hauptdiagonalen.

Die Matrix $ A$ heißt diagonalisierbar, falls es eine invertierbare Matrix $ S\in\mathbb{C}^{n\times n}$ gibt mit $ S^{-1}AS=D$ für eine Diagonalmatrix $ D\in\mathbb{C}^{n\times n}$ , d.h. alle Einträge von $ D$ außerhalb der Diagonalen sollen gleich Null sein. Eine Diagonalmatrix ist eine spezielle Jordanform, in welcher alle Jordanblöcke Größe $ 1$ besitzen.

Die Matrix $ A$ ist diagonalisierbar genau dann, wenn für jeden Eigenwert von $ A$ seine geometrische Vielfachheit gleich seiner algebraischen Vielfachheit ist.

Ist $ A$ als diagonalisierbar bekannt, so vereinfacht sich der Algorithmus zur Findung der Jordanform dahingehend, daß man lediglich Basen der Eigenräume von $ A$ finden muß. In diesem Falle sind die Spalten von $ S$ die gefundenen Basisvektoren der Eigenräume, und die Diagonaleinträge von $ D$ sind die Eigenwerte in entsprechender Reihenfolge.

(Autoren: Künzer/Martin/Tentler/Wahrheit)

siehe auch:

[Beispiele]
  automatisch erstellt am 22.  8. 2006