Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
Mathematik-Online:

Mittelwertsatz und der Satz von Taylor

A B C D E F G H I J K L M N O P Q R S T U V W X Y Z Übersicht

Mittelwertsatz.

Es seien $ n\ge 1$ , $ M\subseteq\mathbb{R}^n$ eine offene Menge und $ f:M\to\mathbb{R}$ differenzierbar.

Es seien ferner $ x,y\in M$ derart, daß die Verbindungsstrecke

$\displaystyle \overline{x,y}:=\{(1-\lambda)x+\lambda y\;\vert\; \lambda\in[0,1]\}$

in $ M$ enthalten ist.

Dann besagt der Mittelwertsatz, daß es ein $ \xi\in\overline{x,y}$ gibt mit

$\displaystyle f(y)-f(x)=f'(\xi)(y-x)\;.$

Gebiete.

Es seien $ n\ge 1$ , $ M\subseteq\mathbb{R}^n$ eine Menge, und $ x,\, y\,\in\, M$ .

Unter einer Kurve in $ M$ von $ x$ nach $ y$ versteht man eine stetige Abbildung $ \gamma:[0,1]\to M$ mit $ \gamma(0)=x$ und $ \gamma(1)=y$ .

Ist z.B. $ \overline{x,y}\subseteq M$ , so ist $ [0,1]\to M,\; \lambda\mapsto (1-\lambda)x+\lambda y$ eine Kurve in $ M$ von $ x$ nach $ y$ .

Eine Menge $ M\subseteq\mathbb{R}^n$ derart, daß für alle $ x,y\in M$ eine Kurve in $ M$ von $ x$ nach $ y$ existiert, heißt zusammenhängend. Ein Gebiet ist eine offene, zusammenhängende Menge.

Eine Menge $ M\subseteq\mathbb{R}^n$ derart, daß für alle $ x,y\in M$ die Verbindungsstrecke $ \overline{x,y}$ in $ M$ liegt, heißt konvex. Ist $ M$ konvex, so ist $ M$ auch zusammenhängend.

Es seien $ M\subseteq\mathbb{R}^n$ ein Gebiet und $ f:M\to\mathbb{R}$ differenzierbar mit $ f'(x)=0$ für alle $ x\in M$ . Dann ist $ f$ konstant, i.e. es ist $ f(x) = f(y)$ für alle $ x,\, y\,\in\, M$ .

Satz von Taylor.

Sei $ M\subseteq\mathbb{R}^n$ offen. Sei $ f:M\to\mathbb{R}$ eine $ (m+1)$ -fach stetig differenzierbare Funktion.

Unter einem Multiindex verstehen wir ein Tupel $ i=(i_1,\ldots,i_n)\in\mathbb{N}^n$ .

Wir setzen

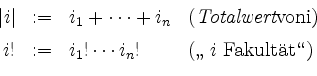
\begin{displaymath} \begin{array}{rcll} \vert i\vert & := & i_1+\cdots+i_n & \ma... ...\cdots i_n! & \mbox{(''\lq $\; i$\ Fakult''at''')} \\ \end{array}\end{displaymath}

Ferner setzen wir im Falle $ \vert i\vert\le m+1$

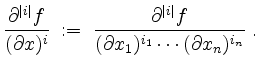
$\displaystyle \dfrac{\partial^{\vert i\vert} f}{(\partial x)^i} \; :=\; \dfrac{\partial^{\vert i\vert} f}{(\partial x_1)^{i_1}\cdots(\partial x_n)^{i_n}}\; . $

Seien schließlich $ x\in M$ und $ h= (h_1,\ldots,h_n)^\mathrm{t}\in\mathbb{R}^n$ . Wir setzen

$\displaystyle h^i \;:=\; h_1^{i_1}\cdots h_n^{i_k}\;. $

Das $ m$ -te Taylorpolynom von $ f:M\longrightarrow\mathbb{R}$ an der Stelle $ x\in\mathbb{R}^n$ in der Variablen $ h\in\mathbb{R}^n$ ist definiert durch

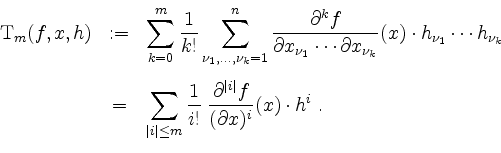
\begin{displaymath} \begin{array}{rcl} \mathrm{T}_m(f,x,h) &:=& \displaystyle\su... ...al^{\vert i\vert} f}{(\partial x)^i}(x)\cdot h^i\;. \end{array}\end{displaymath}

Es ist ein Polynom von Totalgrad $ \le m$ in der Variablen $ h\in\mathbb{R}^n$ , i.e. in den Variablen $ h_1,\ldots,h_n$ .

Beachte, daß in der ersteren Summendarstellung die Indizes $ \nu_1,\ldots,\nu_k$ nicht notwendig paarweise verschieden sind. Ferner tauchen dank des Satzes von Schwarz darin Terme mehrfach auf. In der zweiten Summendarstellung sind diese mehrfachen Terme zusammengefaßt.

Sei nun $ h\in\mathbb{R}^n$ derart, daß $ \overline{x,x+h}\subseteq M$ . Dann besagt der Satz von Taylor, daß es solch ein $ \xi\in\overline{x,x+h}$ gibt, daß

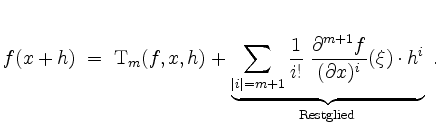
$\displaystyle f(x+h) \;=\; \mathrm{T}_m(f,x,h) + \underbrace{\sum_{\vert i\vert... ...al^{m+1} f}{(\partial x)^i}(\xi)\cdot h^i}_{\mathrm{\scriptsize Restglied}}\;. $

Beachte, daß es ein $ \lambda\in [0,1]$ gibt mit $ \xi = x + \lambda h$ .

Der Mittelwertsatz ist der Spezialfall $ m = 1$ des Satzes von Taylor.

Wir erhalten z.B. die Taylorpolynome

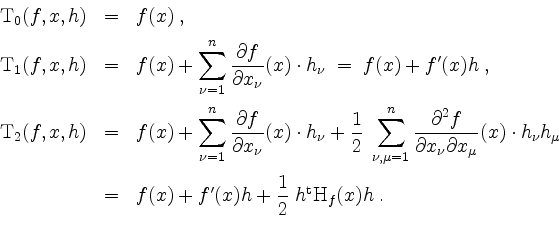
\begin{displaymath} \begin{array}{rcl} \mathrm{T}_0(f,x,h) &=& f(x)\;,\vspace*{2... ...x)h+\dfrac{1}{2}\; h^\mathrm{t}\mathrm{H}_f(x)h\;. \end{array}\end{displaymath}

Genauer ist mit dem Satz von Taylor

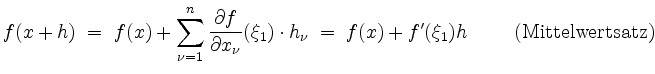
$\displaystyle f(x+h) \;=\; f(x)+\displaystyle\sum_{\nu=1}^{n}\dfrac{\partial f}... ...\xi_1)\cdot h_\nu \;=\; f(x)+f'(\xi_1)h\hspace*{1cm} \mathrm{(Mittelwertsatz)} $

bzw.

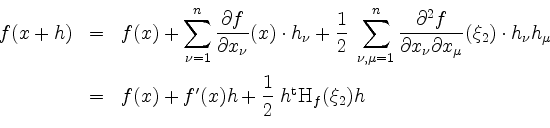
\begin{displaymath} \begin{array}{rcl} f(x+h) &=& f(x)+\displaystyle\sum_{\nu=1}... ...x)h+\dfrac{1}{2}\; h^\mathrm{t}\mathrm{H}_f(\xi_2)h \end{array}\end{displaymath}

bzw.

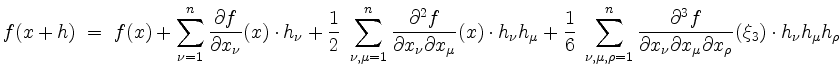
$\displaystyle f(x+h) \;=\; f(x)+\displaystyle\sum_{\nu=1}^{n}\dfrac{\partial f... ...}{\partial x_\nu\partial x_\mu \partial x_\rho}(\xi_3)\cdot h_\nu h_\mu h_\rho $

mit gewissen, nicht näher bekannten, und i.a. verschiedenen Zwischenpunkten $ \xi_1,\, \xi_2,\,\xi_3\,\in\,\overline{x,x+h}$ .
(Autoren: Künzer/Martin/Tentler/Wahrheit)
[Beispiele] [Verweise]
  automatisch erstellt am 11.  8. 2006