Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
Mathematik-Online:

Implizite Funktionen

A B C D E F G H I J K L M N O P Q R S T U V W X Y Z Übersicht

Begriff.

Seien $ m,\, n\,\ge\, 1$ , und seien $ U\subseteq\mathbb{R}^n$ , $ V\subseteq\mathbb{R}^m$ und $ f:U\times V\to\mathbb{R}^m$ gegeben. Sei ferner $ (x_0,y_0)^\mathrm{t}\in U\times V$ , bestehend aus inneren Punkten $ x_0\in U$ und $ y_0\in V$ , derart gegeben, daß $ f(x_0,y_0)=0$ .

Wir sagen, die Gleichung $ f(x,y)=0$ , $ x\in U$ , $ y\in V$ , ist um den Punkt $ (x_0,y_0)^\mathrm{t}$ lokal eindeutig nach $ y$ auflösbar, falls es Umgebungen $ U_0\subseteq U$ von $ x_0$ und $ V_0\subseteq V$ von $ y_0$ so gibt, daß es zu jedem $ x\in U_0$ genau ein $ y\in V_0$ gibt mit $ f(x,y)=0$ . Dadurch wird genau eine Funktion $ g:U_0\to V_0$ definiert, welche $ f(x,g(x))=0$ erfüllt für alle $ x\in U_0$ . Man sagt, die Funktion $ y=g(x)$ ist implizit definiert durch die Gleichung $ f(x,y)=0$ .

Existenz der implizit definierten Funktion.

Es seien nun zusätzlich $ U$ und $ V$ offen, und $ f:U\times V\to\mathbb{R}^m$ einmal stetig differenzierbar. Wir schreiben $ (x,y)^\mathrm{t} =: (x_1,\ldots,x_n,y_1,\ldots,y_m)^\mathrm{t} \in U\times V$ und

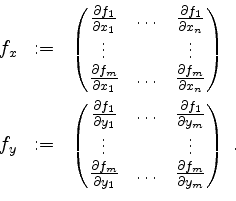
\begin{displaymath} \begin{array}{rcl} f_x &:=& \begin{pmatrix}\frac{\partial f... ... \frac{\partial f_m}{\partial y_m} \end{pmatrix}\;. \end{array}\end{displaymath}

Der Satz über implizite Funktionen besagt nun, daß aus $ \det f_y(x_0,y_0)\ne 0$ folgt, daß die Gleichung $ f(x,y)=0$ um den Punkt $ (x_0,y_0)^\mathrm{t}$ lokal eindeutig nach $ y$ auflösbar ist.

Es gibt dann eine Umgebung $ x_0\in U_0\subseteq U$ so, daß für die implizit definierte Funktion $ g:U_0\to V_0$ folgendes zutrifft.

Man kann $ g'$ auf dieser Umgebung $ U_0$ wie folgt mit Hilfe der Kettenregel gewinnen.

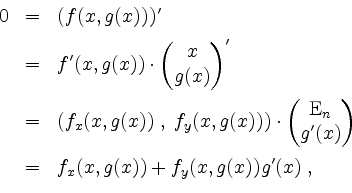
\begin{displaymath} \begin{array}{rcl} 0 &=& (f(x,g(x)))' \vspace*{2mm}\\ &=& ... ...ace*{2mm}\\ &=& f_x(x,g(x)) + f_y(x,g(x)) g'(x)\;, \end{array}\end{displaymath}

und also

$\displaystyle g'(x) \;=\; - f_y(x,g(x))^{-1} f_x(x,g(x)) \; \in\; \mathbb{R}^{m\times n}\; . $

(Autoren: Künzer/Martin/Tentler/Wahrheit)

Beispiele:

[Verweise]
  automatisch erstellt am 11.  8. 2006