
Mathematik-Online:

|
[Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen] |
|
Mathematik-Online: | |
Flächen und Oberflächenintegrale |
| A B C D E F G H I J K L M N O P Q R S T U V W X Y Z | Übersicht |
Sei
![]() eine kompakte meßbare Menge.
eine kompakte meßbare Menge.
Eine Fläche (im dreidimensionalen Raum) ist eine Funktion
![]() derart, daß es eine offene Obermenge
derart, daß es eine offene Obermenge
![]() gibt und sich
gibt und sich ![]() fortsetzen läßt zu einer stetig differenzierbaren Funktion
fortsetzen läßt zu einer stetig differenzierbaren Funktion
![]() .
.
Der Grund für die Forderung der Existenz der größeren Menge ![]() und der Fortsetzung
und der Fortsetzung
![]() ist,
daß wir auch in Randpunkten von
ist,
daß wir auch in Randpunkten von ![]() die Ableitung von
die Ableitung von ![]() betrachten wollen.
Kurz gesagt, ist
betrachten wollen.
Kurz gesagt, ist
![]() eine ,,auch auf dem Rand von
eine ,,auch auf dem Rand von ![]() `` stetig differenzierbare Funktion.
`` stetig differenzierbare Funktion.
Die Bildmenge
![]() heißt der Träger von
heißt der Träger von ![]() .
.
Der Normalenvektor
![]() der Fläche
der Fläche ![]() ist an jedem Punkt
ist an jedem Punkt
![]() definiert durch
definiert durch
Wir erinnnern dabei an die Definition des Kreuzproduktes
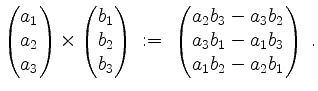
Das Kreuzprodukt zweier Vektoren ist ein Vektor, der zu beiden Faktoren orthogonal ist, und dessen Länge dem Flächeninhalt des von den beiden Faktoren aufgespannten Parallelogramm entspricht.
Oberflächenintegral eines Vektorfeldes.
Es sei
![]() ein stetiges Vektorfeld. Dann definieren wir das
Oberflächenintegral von
ein stetiges Vektorfeld. Dann definieren wir das
Oberflächenintegral von ![]() über
über ![]() vermöge
vermöge
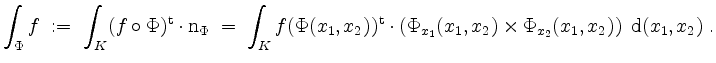
Oberflächenintegral einer skalaren Funktion.
Es sei
![]() eine stetige skalare Funktion. Dann definieren wir das Oberflächenintegral
von
eine stetige skalare Funktion. Dann definieren wir das Oberflächenintegral
von ![]() über
über ![]() vermöge
vermöge
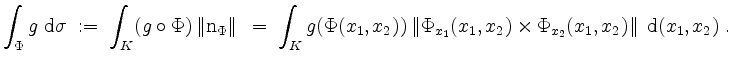
Das Integrationselement
![]() steht dabei für die Integration über eine Fläche, englisch
,,surface``.
steht dabei für die Integration über eine Fläche, englisch
,,surface``.
So ist z.B. der Flächeninhalt der Fläche ![]() definiert als
definiert als
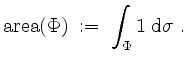
Das Oberflächenintegral ist in gewissem Sinne nur abhängig vom Träger
![]() und von der Orientierung der Fläche. Genauer, ist
und von der Orientierung der Fläche. Genauer, ist
![]() eine weitere kompakte
meßbare Menge,
eine weitere kompakte
meßbare Menge,
![]() eine stetig differenzierbare Funktion, und ist
eine stetig differenzierbare Funktion, und ist
![]() eine stetig differenzierbare bijektive Abbildung so, daß
eine stetig differenzierbare bijektive Abbildung so, daß
![]() und
und
![]() überall, so heißen
die Flächen
überall, so heißen
die Flächen ![]() und
und
![]() äquivalent. Es gelten dann
äquivalent. Es gelten dann
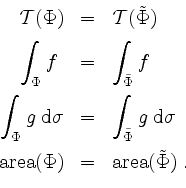
Der Kurvenschwerpunkt und die 2. Guldinsche Regel.
Sei
![]() ein Weg mit
ein Weg mit
![]() .
Dann heißt der Punkt
.
Dann heißt der Punkt
![]() mit den Koordinaten
mit den Koordinaten
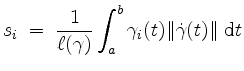
der Kurvenschwerpunkt von
Sei nun speziell
![]() ein Weg mit Kurvenschwerpunkt
ein Weg mit Kurvenschwerpunkt
![]() .
Sei
.
Sei ![]() die aus
die aus ![]() entstehende Rotationsfläche bei Drehung um die
entstehende Rotationsfläche bei Drehung um die ![]() -Achse, d.h.
-Achse, d.h. ![]() ist die
Fläche mit der Parametrisierung
ist die
Fläche mit der Parametrisierung
Der 2. Guldinschen Regel zufolge berechnet sich nun den Flächeninhalt von
Mit anderen Worten, der Flächeninhalt der Rotationsfläche
Beispiele:
| automatisch erstellt am 11. 8. 2006 |