Mathematik-Online: Fouriertransformation

	[Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
	Mathematik-Online:
	Fouriertransformation

A B C D E F G H I J K L M N O P Q R S T U V W X Y Z

Übersicht

Definition.

Sei $f:\mathbb{R}\to\mathbb{C}$ so gegeben, daß $e^{-\mathrm{i}\omega t} f(t)$ für alle $\omega\in\mathbb{R}$ von $-\infty$ bis $+\infty$ integrierbar ist. Es heiße in diesem Falle fouriertransformierbar, und die resultierende Funktion

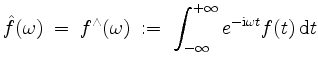
$\displaystyle \hat{f}(\omega) \; =\; f^\wedge(\omega) \; := \; \int_{-\infty}^{+\infty} e^{-\mathrm{i}\omega t} f(t) \,\mathrm{d}t$

in $\omega\in\mathbb{R}$ die Fouriertransformierte von

. Die Bezeichnungen $\hat{f}$ und $f^\wedge$ seien gleichbedeutend, erstere ist nicht immer praktisch.

Wir erlauben uns bei Bedarf auch, $[f(t)]^\wedge(\omega) := \hat{f}(\omega)$ zu schreiben. Das Argument diene hierbei nur der Kenntlichmachung der fourierzutransformierenden Funktion, das Resultat ist weiterhin eine Funktion in $\omega$ .

Ist stückweise stetig und ist $\vert f(t)\vert$ von $-\infty$ bis $+\infty$ integrierbar ist, so heiße absolut integrierbar. Absolut integrierbare Funktionen sind fouriertransformierbar.

Regeln.

Seien $f,\, g :\mathbb{R}\to\mathbb{C}$ fouriertransformierbar. Seien $\alpha,\,\beta\,\in\,\mathbb{C}$ . Sei $r\in\mathbb{R}$ . Sei $m\,\ge\, 0$ ganz.

Folgende Gleichheiten gelten für alle $\omega\in\mathbb{R}$ .

Es ist $(\alpha f + \beta g)^\wedge(\omega) = \alpha \hat{f}(\omega) + \beta \hat{g}(\omega)$ .
Es ist $[\overline{f(t)}]^\wedge(\omega) = \overline{\hat{f}(-\omega)}$ .
Es ist $[f(-t)]^\wedge(\omega) = \hat{f}(-\omega)$ .
Es ist $[f(rt)]^\wedge(\omega) = \hat{f}(\omega/r)/r$ , falls .
Es ist $[f(t-r)]^\wedge(\omega) = e^{-\mathrm{i}\omega r}\hat{f}(\omega)$ .
Es ist $[f^{(m)}(t)]^\wedge(\omega) = (\mathrm{i}\omega)^m \hat{f}(\omega)$ , falls -fach differenzierbar ist.
Es ist $[t^m f(t)]^\wedge(\omega) = \mathrm{i}^m \hat{f}^{(m)}(\omega)$ , falls fouriertransformierbar ist.
Es ist $[e^{\mathrm{i} rt} f]^\wedge(\omega) = \hat{f}(\omega - r)$ .
Es ist $(f^\wedge)^\wedge(t) = 2\pi\cdot f(-t)$ für $t\in\mathbb{R}$ , falls absolut integrierbar und stetig differenzierbar ist.
Ist hingegen nur stückweise stetig differenzierbar, und existieren an jeder Sprungstelle die einseitigen Grenzwerte von und von , so gilt die Formel weiterhin, mit der Modifikation, daß an den Sprungstellen von die Funktion $(f^\wedge)^\wedge(t)$ den (arithmetischen) Mittelwert der einseitigen Grenzwerte von $2\pi\cdot f(-t)$ als Wert annimmt.

Sei erwähnt, daß bei Fouriertransformationen in der Praxis häufig mit verallgemeinerten Funktionen, sogenannten Distributionen, gerechnet wird. So etwa ist die Fouriertransformierte der konstanten Funktion das $2\pi$ -fache des Diracschen $\delta$ . Wir wollen uns dagegen auf Funktionen im eigentlichen Sinne beschränken.

Faltung.

Seien $f,\, g :\mathbb{R}\to\mathbb{C}$ absolut integrierbar. Sei die Funktion

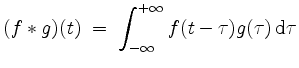
$\displaystyle (f\ast g)(t) \; =\; \int_{-\infty}^{+\infty} f(t - \tau) g(\tau) \,\mathrm{d}\tau$

in $t\in\mathbb{R}$ die Faltung von

und

. Als Merkregel beobachte man, daß das Integral an das Cauchyprodukt von Reihen erinnert.

Dann ist

$\displaystyle (f\ast g)^\wedge(\omega) \; =\; \hat{f}(\omega)\cdot \hat{g}(\omega)$

für $\omega\in\mathbb{R}$ .

Parseval.

Ist $f:\mathbb{R}\to\mathbb{C}$ absolut integrierbar, so gilt die Parsevalsche (Norm-)Gleichung

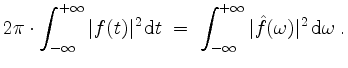
$\displaystyle 2\pi\cdot\int_{-\infty}^{+\infty} \vert f(t)\vert^2\,\mathrm{d}t \; =\; \int_{-\infty}^{+\infty} \vert\hat{f}(\omega)\vert^2\,\mathrm{d}\omega\; .$

Poisson.

Ist $f:\mathbb{R}\to\mathbb{C}$ absolut integrierbar, so gilt die Poissonsche Summationsformel

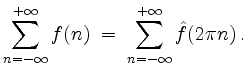
$\displaystyle \sum_{n = -\infty}^{+\infty} f(n) \; =\; \sum_{n = -\infty}^{+\infty} \hat{f}(2\pi n)\; .$

(Autoren: Künzer/Martin/Tentler/Wahrheit)

[Beispiele] [Verweise]

automatisch erstellt am 11. 8. 2006