Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
Mathematik-Online-Kurs: Analysis einer Veränderlichen - Konvergenz und Grenzwerte - Reihen

Reihen in Maple

[vorangehende Seite] [nachfolgende Seite] [Gesamtverzeichnis][Seitenübersicht]
Möchte man eine endliche Summe von expliziten Werten berechnen, so benützt man in MAPLE vorzugsweise den Befehl add. Der Befehl sum ist dagegen geeignet für symbolische Summationen, z.B. um eine Formel für $ \sum_{k=1}^n k$ zu erhalten. Kann MAPLE keine geschlossene Form für die Summe finden, so wird der Funktionsaufruf selbst zurückgegeben. Bei sum wird empfohlen, sowohl die Summanden, als auch die Zählvariable in einfachen Anführungszeichen ` anzugeben.

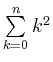Die Summe $ \sum\limits_{k=0}^{100} k$ lässt sich wie folgt mit add berechnen, für $ \sum\limits_{k=0}^{n} k$ und $ \sum\limits_{k=0}^{n} k^2$ dagegen erhält man nur mit sum eine Lösung.

> add(k, k=0..100);

$\displaystyle 5050 $

> add(k, k=0..n);

Error, unable to execute add

> sum('k', 'k'=1..n);

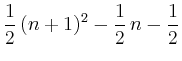
$\displaystyle {\displaystyle \frac {1}{2}} \,(n + 1)^{2} - {\displaystyle \frac {1}{2}} \,n - {\displaystyle \frac {1}{2}} $

> sum('k^2', 'k'=1..n);

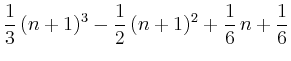
$\displaystyle {\displaystyle \frac {1}{3}} \,(n + 1)^{3} - {\displaystyle \fr... ...+ 1)^{2} + {\displaystyle \frac {1}{6}} \,n + {\displaystyle \frac {1}{6}} $

Mit dem Befehl sum lassen sich auch Werte von unendlichen Reihen berechnen.

> sum('x^k/k!', 'k'=0..infinity);

$\displaystyle e^{x} $

> sum('1/k', 'k'=1..infinity);

$\displaystyle \infty $

> sum('1/k^2', 'k'=1..infinity);

$\displaystyle {\displaystyle \frac {1}{6}} \,\pi ^{2} $

> sum('(-1)^k/(k^4)', k=1..infinity);

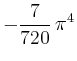
$\displaystyle - {\displaystyle \frac {7}{720}} \,\pi ^{4} $

(Autor: Marcus Reble)
[vorangehende Seite] [nachfolgende Seite] [Gesamtverzeichnis][Seitenübersicht]
  automatisch erstellt am 5.1.2017