Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
Mathematik-Online-Kurs: Analysis einer Veränderlichen - Differentiation - Anwendungen

Regel von l'Hospital

[vorangehende Seite] [nachfolgende Seite] [Gesamtverzeichnis][Seitenübersicht]
Haben zwei stetig differenzierbare Funktionen $ f$ und $ g$ eine gemeinsame Nullstelle oder Polstelle in $ a$ , so gilt

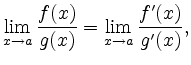
$\displaystyle \lim_{x\to a}\frac{f(x)}{g(x)} = \lim_{x\to a}\frac{f'(x)}{g'(x)} , $

falls der rechte Grenzwert existiert (gegebenenfalls im uneigentlichen Sinn).
(Inhalt vorübergehend nicht verfügbar)
Die Anwendung der Regel von l'Hospital wird anhand einer Reihe von Beispielen illustriert.

Fall $ 0/0$:

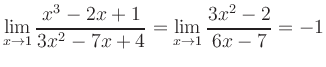
$\displaystyle \lim_{x\to 1} \frac{x^3 -2x +1}{3x^2-7x+4} = \lim_{x\to 1}\frac{3x^2-2}{6x-7} = -1$


Fall $ -\infty/\infty$:

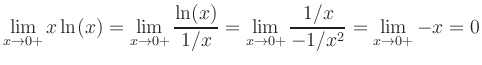
$\displaystyle \lim_{x \to 0+} x\ln(x)= \lim_{x \to 0+} \frac{\ln(x)}{1/x} = \lim_{x \to 0+} \frac{1/x}{-1/x^2} = \lim_{x \to 0+} -x =0$


Fall $ x \to \infty$:

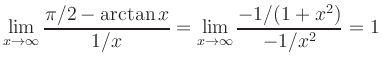
$\displaystyle \lim_{x\to\infty} \frac{\pi/2-\arctan x}{1/x} = \lim_{x\to\infty} \frac{-1/(1+x^2)}{-1/x^2} = 1 $

mehrfache Anwendung:
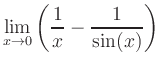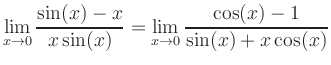$\displaystyle \lim_{x \to 0} \left( \frac{1}{x} - \frac{1}{\sin(x)}\right)$ $\displaystyle =$ $\displaystyle \lim_{x \to 0} \frac{\sin(x)-x}{x\sin(x)}= \lim_{x \to 0} \frac{\cos(x)-1}{\sin(x)+x\cos(x)}$  
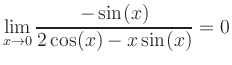  $\displaystyle =$ $\displaystyle \lim_{x \to 0} \frac{-\sin(x)}{2\cos(x)-x\sin(x)} = 0$  

Bei den Beispielen ist zu beachten, dass die Existenz der zu berechnenden Grenzwerte erst durch die Existenz der nach Anwendung der Regel von l'Hospital enstehenden Grenzwerte gesichert ist.

[vorangehende Seite] [nachfolgende Seite] [Gesamtverzeichnis][Seitenübersicht]
  automatisch erstellt am 5.1.2017