Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen] Englische Flagge
Mathematik-Online-Kurs: Lineare Algebra - Normalformen - Eigenwerte und Eigenvektoren

Berechnung von Eigenwerten und -vektoren

[vorangehende Seite] [nachfolgende Seite] [Gesamtverzeichnis][Seitenübersicht]
Um das Eigenwertproblem für eine quadratische Matrix $ A$ zu lösen, bestimmt man zunächst die Eigenwerte $ \lambda$ als Nullstellen des charakteristischen Polynoms

$\displaystyle p_A( \lambda ) = \operatorname{det} (A - \lambda E)\,. $

Für jeden Eigenwert $ \lambda$ erhält man die dazu gehörigen Eigenvektoren $ v$ als nichttriviale Lösungen des homogenen linearen Gleichungssystems

$\displaystyle (A - \lambda E) v = 0\,. $

Um eine Basis für den Eigenraum $ V_{\lambda}$ zu erhalten, kann man das System auf Echelon-Form transformieren.

Im allgemeinen ist $ \operatorname{dim} V_{\lambda} = 1$. Der bis auf einen skalaren Faktor eindeutig bestimmte Eigenvektor $ v$ kann dann bestimmt werden, indem man eine geeignete Komponente von $ v$ vorgibt.

Zur Bestimmung der Eigenwerte der Matrix

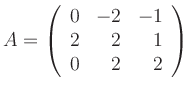
$\displaystyle A=\left(\begin{array}{rrr}0& -2 &-1\\ 2 & 2 & 1 \\ 0 & 2& 2\end{array}\right) $

bildet man das charakteristische Polynom

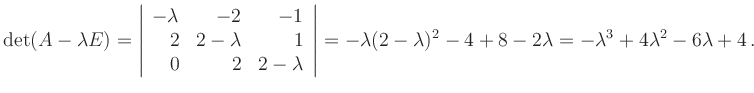
$\displaystyle \operatorname{det}(A-\lambda E)=\left\vert\begin{array}{rrr}-\lam... ...t = -\lambda(2-\lambda)^2-4+8-2\lambda = -\lambda^3+4\lambda^2-6\lambda+4\,. $

und bestimmt dessen Nullstellen. Durch Raten (Teiler des Absolutgliedes) erhält man als erste Nullstelle $ \lambda_1=2$. Abdividieren des Linearfaktors zu dieser Nullstelle,

$\displaystyle (-\lambda^3+4\lambda^2-6\lambda+4)/(\lambda-2)=-\lambda^2+2\lambda-2, $

und Einsetzen in die Lösungsformel für quadratische Gleichungen ergibt

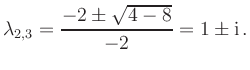
$\displaystyle \lambda_{2,3}=\frac{-2\pm \sqrt{4-8}}{-2}=1\pm \mathrm{i}\,. $

Ein Eigenvektor zum Eigenwert $ 2$ lässt sich über die Lösung des homogenen Gleichungssystems

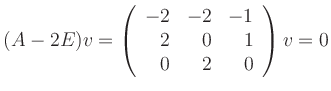
$\displaystyle (A-2 E)v=\left(\begin{array}{rrr}-2& -2 &-1\\ 2 & 0 & 1 \\ 0 & 2 & 0\end{array}\right)v =0 $

bestimmen. Die Lösung $ v=(1,0,-2)^{\operatorname t}$ ist leicht zu sehen.

Ein Eigenvektor $ w_1$ zum Eigenwert $ 1+\mathrm{i}$ erhält man aus

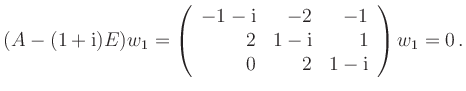
$\displaystyle (A-(1+\mathrm{i})E)w_1=\left(\begin{array}{rrr}-1-\mathrm{i}& -2 &-1\\ 2 & 1-\mathrm{i} & 1 \\ 0 & 2 & 1-\mathrm{i}\end{array}\right)w_1 =0\,. $

und somit z.B. $ w_1=(-1-\mathrm{i}, -1+\mathrm{i}, 2)^{\operatorname t}$. Da $ A$ reell ist, kann der Eigenvektor zu $ \lambda=1-\mathrm{i}$ durch komplexe Konjugation gebildet werden: $ w_2= \overline{w_1} =(-1+\mathrm{i}, -1-\mathrm{i}, 2)^{\operatorname t}$.
[vorangehende Seite] [nachfolgende Seite] [Gesamtverzeichnis][Seitenübersicht]
  automatisch erstellt am 14.6.2012