Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
Mathematik-Online-Kurs: Differentialrechnung mehrerer Veränderlicher - Funktionen

Multivariate Funktionen

[vorangehende Seite] [nachfolgende Seite] [Gesamtverzeichnis][Seitenübersicht]
Eine reelle multivariate Funktion (auch als Funktion von mehreren Veränderlichen bezeichnet)

$\displaystyle f:\mathbb{R}^n \supseteq D \to \mathbb{R}^m,\quad x\mapsto f(x)\, , $

ordnet einem Vektor $ x = (x_1,\ldots,x_n)^{\operatorname t}$ aus dem Definitionsbereich $ D$ einen Vektor $ f(x) = f(x_1, \ldots, x_n) = (f_1(x),\ldots,f_m(x))^{\operatorname t}$ zu, $ f$ hängt also von $ n$ reellen Veränderlichen $ x_1, \ldots , x_n $ ab.

Je nach Dimension $ m$ des Bildbereichs unterscheidet man zwischen skalaren $ (m=1)$ und vektorwertigen $ (m>1)$ Funktionen. Ist $ n = 1$ (und $ f$ stetig), so nennt man $ f$ eine Parametrisierung einer Kurve.

Für $ m,n \le 3$ verwendet man meist keine Indizes und bezeichnet die Variablen mit $ x, y $ und $ z .$

Beispielsweise schreibt man

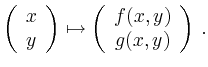
$\displaystyle \left(\begin{array}{c}x\\ y\end{array}\right) \mapsto \left(\begin{array}{c}f(x,y)\\ g(x,y)\end{array} \right) \,. $

im Fall $ m=n=2$.

\includegraphics[width=0.4\linewidth]{bild1_skalare_funktion} \includegraphics[width=0.4\linewidth]{bild2_skalare_funktion}

Wie in der Abbildung illustriert, können zur Visualisierung skalarer Funktionen der Graph

$\displaystyle \{(x,f(x)):\ x\in D\} $

und die Niveauflächen

$\displaystyle \{x\in D:\ f(x)=c\} $

benutzt werden.

[vorangehende Seite] [nachfolgende Seite] [Gesamtverzeichnis][Seitenübersicht]
  automatisch erstellt am 5.1.2017