Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
Mathematik-Online-Kurs: Repetitorium HM III - Funktionentheorie

Laurentreihen, Singularitäten

[vorangehende Seite] [nachfolgende Seite] [Gesamtverzeichnis][Seitenübersicht]

Funktionen, die nicht mehr auf einer vollen Kreisscheibe, sondern nur noch auf einem Kreisring holomorph sind, kann man unter Hinzunahme negativer Glieder immer noch um den Mittelpunkt in eine Reihe entwickeln, in eine sogenannte Laurentreihe.

Sei $ \mbox{$R > r \geq 0$}$, sei $ \mbox{$z_0\in\mathbb{C}$}$, sei $ \mbox{$B_{R,r}(z_0) := \{ z\in\mathbb{C}\; \vert\; r < \vert z - z_0\vert < R \}$}$ ein offener Kreisring. Desweiteren sei $ \mbox{$B_{\infty,r}(z_0) := \{ z\in\mathbb{C}\; \vert\; r < \vert z - z_0\vert\}$}$, und sei $ \mbox{$R = \infty$}$ ebenfalls zugelassen. In der Anwendung ist häufig $ \mbox{$r = 0$}$, d.h. es liegt eine gelochte Kreissscheibe vor.

Sei $ \mbox{$f: B_{R,r}(z_0)\longrightarrow \mathbb{C}$}$ eine holomorphe Funktion. Sei $ \mbox{$r < \rho < R$}$, und sei $ \mbox{$\gamma(t) = z_0 + \rho e^{it}$}$ für $ \mbox{$t\in [0,2\pi]$}$. Für $ \mbox{$n\in\mathbb{Z}$}$ sei

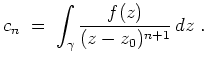
$ \mbox{$\displaystyle c_n\; =\; \int_\gamma \frac{f(z)}{(z - z_0)^{n+1}}\, dz\; . $}$
Dann ist auf $ \mbox{$B_{R,r}(z_0)$}$
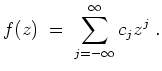
$ \mbox{$\displaystyle f(z)\; =\; \sum_{j = -\infty}^\infty c_j z^j\; . $}$
Diese Entwicklung ist eindeutig. Findet man also unter Zuhilfenahme etwa einer Partialbruchzerlegung eine derartige Entwicklung einer Funktion auf einem gewissen offenen Kreisring um $ \mbox{$z_0$}$ in $ \mbox{$B_{R,r}(z_0)$}$, so hat man die Laurentreihe bestimmt, ohne die Integrale tatsächlich ausrechnen zu müssen.

Ist $ \mbox{$r = 0$}$, so heißt $ \mbox{$z_0$}$ isolierte Singularität von $ \mbox{$f$}$. Man unterscheidet $ \mbox{$3$}$ Arten solcher Singularitäten.

Ist $ \mbox{$c_j = 0$}$ für alle $ \mbox{$j < 0$}$, so ist $ \mbox{$f$}$ zu einer holomorphen Funktion auf der ungelochten Kreisscheibe $ \mbox{$B_R(z_0)$}$ fortsetzbar. Dementsprechend heißt $ \mbox{$z_0$}$ hebbare Singularität von $ \mbox{$f$}$.

Ist $ \mbox{$z_0$}$ keine hebbare Singularität, wird aber die Folge $ \mbox{$c_{-1}$}$, $ \mbox{$c_{-2}$}$, ... noch irgendwann konstant Null, so heißt $ \mbox{$z_0$}$ Pol von $ \mbox{$f$}$. Das größte $ \mbox{$N$}$ mit $ \mbox{$c_{-N}\neq 0$}$ gibt seine Ordnung an. Diesenfalls gibt es für jedes $ \mbox{$K\geq 0$}$ ein $ \mbox{$\varepsilon > 0$}$ so, daß $ \mbox{$\vert f(z)\vert > K$}$ für $ \mbox{$z\in B_{\varepsilon ,0}(z_0)$}$, man schreibt $ \mbox{$\lim_{z\to z_0} f(z) = \infty$}$ (uneigentliche Konvergenz).

Wird diese Folge $ \mbox{$c_{-1}$}$, $ \mbox{$c_{-2}$}$, ... nicht irgendwann konstant Null, so heißt $ \mbox{$z_0$}$ wesentliche Singularität von $ \mbox{$f$}$. Dann gilt nach Casorati-Weierstraß, daß es für alle $ \mbox{$w\in\mathbb{C}$}$ und für alle $ \mbox{$\varepsilon ,\delta > 0$}$ ein $ \mbox{$z\in B_{\delta,0}(z_0)$}$ gibt mit $ \mbox{$\vert f(z) - w\vert < \varepsilon $}$. Insbesondere ist $ \mbox{$f(z)$}$ für $ \mbox{$z\to z_0$}$ nicht konvergent, auch nicht uneigentlich.

(Autoren: Künzer/Meister/Nebe)

Beispiele

Aufgaben

  automatisch erstellt am 21.3.2003