Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
Mathematik-Online-Kurs: Repetitorium HM III - Wahrscheinlichkeitsrechnung und Statistik

Konfidenzintervalle

[vorangehende Seite] [nachfolgende Seite] [Gesamtverzeichnis][Seitenübersicht]

Sei $ \mbox{$X_1,\dots,X_n$}$ eine Stichprobe mit zu schätzendem unbekannten Parameter $ \mbox{$\vartheta$}$.

Ein Konfidenzintervall für $ \mbox{$\vartheta$}$ ist ein Zufallsintervall $ \mbox{$[T_u,T_o]$}$, d.h. $ \mbox{$T_u(X_1,\dots,X_n)$}$ und $ \mbox{$T_o(X_1,\dots,X_n)$}$ sind Schätzer für $ \mbox{$\vartheta$}$.

Ein Konfidenzintervall zum Konfidenzniveau $ \mbox{$1-\alpha$}$ mit $ \mbox{$\alpha\in(0,1)$}$ enthält den wahren Parameter $ \mbox{$\vartheta$}$ mit Wahrscheinlichkeit $ \mbox{$1-\alpha$}$. Unter der Annahme, die $ \mbox{$X_i$}$ seien mit Parameter $ \mbox{$\vartheta$}$ verteilt, muß gelten

$ \mbox{$\displaystyle P\bigl(T_u(X_1,\dots,X_n)\leq\vartheta\leq T_o(X_1,\dots,X_n)\bigr)\;\geq\; 1-\alpha. $}$

Es gibt mehrere Möglichkeiten Konfidenzintervalle zu berechnen.

(i)
Sei $ \mbox{$(X_n)_{n\in\mathbb{N}}$}$ ein Folge unabhängiger und $ \mbox{$\Phi_{\mu,\sigma^2}$}$-verteilter Zufallsvariablen mit bekannter Varianz $ \mbox{$\sigma^2$}$ gegeben, so gilt für das symmetrische Konfidenzintervall um $ \mbox{$\mu$}$
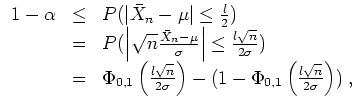
$ \mbox{$\displaystyle \begin{array}{rcl} 1 - \alpha & \leq & P(\vert\bar{X... ...(1 - \Phi_{0,1}\left(\frac{l\sqrt{n}}{2\sigma}\right))\; , \\ \end{array} $}$
und somit
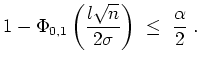
$ \mbox{$\displaystyle 1 - \Phi_{0,1}\left(\frac{l\sqrt{n}}{2\sigma}\right)\;\leq\; \frac{\alpha}{2}\; . $}$
Dabei ist $ \mbox{$\alpha\in(0,1)$}$ die Irrtumswahrscheinlichkeit und $ \mbox{$l$}$ gibt die Länge des Konfidenzintervalls an. Je nach Aufgabenstellung ist der verbleibende Parameter (also entweder $ \mbox{$n$}$ oder $ \mbox{$\alpha$}$ oder $ \mbox{$l$}$) geeignet zu bestimmen.
(ii)
Ist von den $ \mbox{$X_i$}$ nur $ \mbox{${\operatorname{Var}}(X_i) = \sigma^2 > 0$}$ bekannt, so folgt nach dem zentralen Grenzwertsatz, daß $ \mbox{$\sqrt{n}\frac{\bar{X}_n-\mu}{\sigma}$}$ approximativ standardnormalverteilt ist, d.h. Teil (i) wird genauso verwendet.
(iii)
Im Spezialfall binomialverteilter Zufallsvariablen mit unbekanntem Parameter $ \mbox{$p = P(X_i=1)\in(0,1)$}$ ist die Varianz durch $ \mbox{$p(1-p)$}$ gegeben, muß also nicht als bekannt vorausgesetzt werden, sonden geht in die Herleitung als vom unbekannten Parameter $ \mbox{$p$}$ abhängig ein. Das liefert dann aufwendigere Formeln.

Da eine Binomialverteilung nach de Moivre-Laplace nach Normierung in der Grenze gegen die Standardnormalverteilung geht, wird mit $ \mbox{$c = \Phi^{-1}_{0,1}(1-\frac{\alpha}{2})$}$ für große $ \mbox{$n$}$

$ \mbox{$\displaystyle P\left(T_u(X_1,\dots,X_n) \leq p \leq T_o(X_1,\dots,X_n)\right) \;\approx\; 1-\alpha\; , $}$
wobei
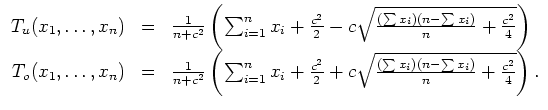
$ \mbox{$\displaystyle \begin{array}{rcl} T_u(x_1,\dots,x_n) &=& \frac{1}{n+c... ...sqrt{\frac{(\sum x_i) (n-\sum x_i)}{n} + \frac{c^2}{4}}\right). \end{array} $}$
Um zu Meßdaten $ \mbox{$x_1,\dots,x_n$}$ ein solches Konfidenzintervall anzugeben, setzt man diese in obige Ausdrücke für $ \mbox{$T_u$}$ und $ \mbox{$T_o$}$ ein, dabei ist $ \mbox{$\sum_{i=1}^n x_i$}$ gerade die Anzahl der Treffer.

(Autoren: Künzer/Meister/Nebe)

Beispiele

Aufgaben

  automatisch erstellt am 21.3.2003