Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
Mathematik-Online-Kurs: Repetitorium HM III - Partielle Differentialgleichungen

Lineare partielle Differentialgleichungen erster Ordnung

[vorangehende Seite] [nachfolgende Seite] [Gesamtverzeichnis][Seitenübersicht]

Problem.

Alle auftretenden Funktionen seien beliebig oft stetig differenzierbar.

Gesucht wird eine Funktion $ \mbox{$u:\mathbb{R}^n\longrightarrow \mathbb{R}$}$, die einer Gleichung der Form

$ \mbox{$\displaystyle (\ast)\rule{4cm}{0cm} \sum_{i\in [1,n]} a_i(x) u_{x_i}(x) + a_0(x) u(x) + c(x) \; =\; 0 $}$
genügt. Hierbei sei $ \mbox{$x = (x_1,\dots,x_n)\in\mathbb{R}^n$}$.

Ist $ \mbox{$c(x) = 0$}$, so heißt die Gleichung homogen.

$ \mbox{$\displaystyle (\ast_H)\rule{4cm}{0cm} \sum_{i\in [1,n]} a_i(x) u_{x_i}(x) + a_0(x) u(x) \; =\; 0 $}$
Hier ist eine beliebige Linearkombination von Lösungen wieder eine Lösung.

Ist dazuhin $ \mbox{$a_0(x) = 0$}$, so spricht man von einer Rumpfgleichung.

$ \mbox{$\displaystyle (\ast_R)\rule{4cm}{0cm} \sum_{i\in [1,n]} a_i(x) u_{x_i}(x) \; =\; 0 $}$
Hier ist die allgemeine Lösung durch eine spezielle Lösung gegeben, zu der noch die allgemeine Lösung von $ \mbox{$(\ast_H)$}$ addiert wird. Dies wird sich auch aus dem Verfahren so ergeben.

Rumpfgleichung.

Wir fragen nach der Form, die eine eindimensional parametrisierte Kurve $ \mbox{$x = x(t)$}$ im $ \mbox{$\mathbb{R}^n$}$ annehmen muß, damit jede Lösung $ \mbox{$u(x)$}$ der Rumpfgleichung auf ihr konstant ist. Fixiert man einen Raumpunkt $ \mbox{$x_0$}$, so wird man i.a. in genau eine Richtung laufen können, ohne den Wert irgendeiner Lösung $ \mbox{$u(x)$}$ zu ändern.

Um $ \mbox{$u(x(t))$}$ konstant zu haben, sollte

$ \mbox{$\displaystyle \frac{d}{dt}u(x(t)) \; =\; \sum_{i\in [1,n]} \dot x_i(t) u_{x_i}(x(t)) \; =\; 0 $}$
sein. Falls also
$ \mbox{$\displaystyle \dot x_i(t) \; =\; a_i(x(t))\hspace*{1cm}{\mbox{f\uml ur alle {$\mbox{$i\in [1,n]$}$}}} $}$
ist, so ist $ \mbox{$u(x(t))$}$ konstant, vorausgesetzt $ \mbox{$u$}$ ist eine Lösung von $ \mbox{$(\ast_R)$}$. Lösungen dieses gewöhnlichen Differentialgleichungssystems heißen Charakteristiken. Eine Charakteristik ist also eine eindimensionale Raumkurve. Umgekehrt, falls $ \mbox{$u$}$ entlang aller Charakteristiken konstant ist, so löst $ \mbox{$u$}$ die Rumpfgleichung, da durch jeden Punkt des $ \mbox{$\mathbb{R}^n$}$ (i.a.) eine Charakteristik läuft, und dort also nach Ersetzung von $ \mbox{$u_{x_i}(x(t))$}$ durch $ \mbox{$\dot x_i(t)$}$ die zu erfüllende Gleichung $ \mbox{$(\ast_R)$}$ in die Konstanzbedingung übergeht.

In der Praxis wählt man ein $ \mbox{$x_j$}$ für ein $ \mbox{$j\in [1,n]$}$ und löst das System

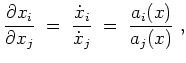
$ \mbox{$\displaystyle \frac{\partial x_i}{\partial x_j}\; =\; \frac{\dot x_i}{\dot x_j}\; =\; \frac{a_i(x)}{a_j(x)}\; , $}$
wobei $ \mbox{$i\in [1,n]\backslash \{ j\}$}$, und worin die $ \mbox{$x_i = x_i(x_j)$}$ als nur vom Parameter $ \mbox{$x_j$}$ abhängige Variablen anzusehen sind. In anderen Worten, man läuft entlang der $ \mbox{$x_j$}$-Achse und fragt nach der aktuellen Position des Kurvenpunktes in den anderen Variablen.

Für die Charakteristiken bestimme man (so auffindbar) notwendige Bedingungen in der impliziten Form

$ \mbox{$\displaystyle f_j(x) \; =\; c_j $}$
mit $ \mbox{$j\in [1,n-1]$}$ so, daß die $ \mbox{$(n-1)\times n$}$-Jacobimatrix $ \mbox{$((f_j)_{x_i})_{j,i}$}$ eine $ \mbox{$(n-1)\times (n-1)$}$-Unterdeterminante hat, die nicht identisch verschwindet. In anderen Worten, man bestimme $ \mbox{$n - 1$}$ unabhängige Bedingungen in impliziter Form. Jedes Konstantentupel $ \mbox{$(c_1,\dots, c_{n-1})$}$ bestimmt dann eine Charakteristik, gegeben als nicht parametrisierte Teilmenge durch $ \mbox{$\{x\in\mathbb{R}^n \; \vert\; f_j(x) = c_j \;\text{ f\uml ur } j\in [1,n-1]\}$}$.

(Sind keine $ \mbox{$n - 1$}$ unabhängigen Lösungen ersichtlich, so kann man durch Einführen von Zusatzbedingungen häufig gewisse Lösungen ermitteln. Wenn man etwa $ \mbox{$u_{x_k} = 0$}$ fordert, und dann eine Lösung erhält, die $ \mbox{$x_k$}$ nicht involviert, so hat man eine Lösung gefunden. Wenn unter dieser Zusatzbedingung aber alle solche Lösungen $ \mbox{$x_k$}$ involvieren, so hat man einen Widerspruch, und so zumindest gezeigt, daß jede Lösung von $ \mbox{$(\ast_R)$}$ echt von $ \mbox{$x_k$}$ abhängt. Mit diesen so gefundenen unabhängigen Partikulärlösungen - i.a. echt weniger als $ \mbox{$n - 1$}$ Stück, d.h. weniger als benötigt - kann man aber zumindest durch eine Substitution die Zahl der Variablen reduzieren. Vgl. auch die Bemerkung am Schluß.)

Für eine beliebige Funktion $ \mbox{$v$}$ in $ \mbox{$(n-1)$}$ Variablen ist dann

$ \mbox{$\displaystyle u\; =\; v(f(x)) \;=\; v\bigl(f_1(x_1,x_2,\dots,x_n),\dots,f_{n-1}(x_1,x_2,\dots,x_n)\bigr) $}$
entlang der Charakteristiken konstant, löst also die Rumpfgleichung.

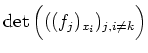Eine Transformation $ \mbox{$\xi_1 = f_1(x_1,x_2,\dots,x_n),\dots, \xi_{n-1} = f_{n-1}(x_1,x_2,\dots,x_n)$}$ und $ \mbox{$\xi_n = x_k$}$ so, daß die unter Streichung der $ \mbox{$k$}$-ten Spalte entstehende oben bereits betrachtete Jacobi-Unterdeterminante $ \mbox{$\det\Big( ((f_j)_{x_i})_{j,i\neq k}\Big)$}$ nicht identisch verschwindet, transformiert die impliziten Bedingungen für die Charakteristiken in $ \mbox{$\xi_j = c_j$}$ für $ \mbox{$j\in [0,n-1]$}$. Eine Funktion, die nun entlang der Charakteristiken konstant ist, ist in der Tat nur noch von $ \mbox{$\xi_1,\dots,\xi_{n-1}$}$ abhängig, und nicht mehr von $ \mbox{$\xi_n$}$. Dies zeigt, daß jede Lösung unserer Rumpfgleichung von der oben beschriebenen Form ist.

Allgemeiner Fall.

Für $ \mbox{$(\ast)$}$ setze man nun für eine Koordinatentransformation

$ \mbox{$\displaystyle \xi \; =\; \xi(x)\; ,\hspace*{1cm} x = x(\xi) $}$
an, wobei $ \mbox{$\xi = (\xi_1,\dots,\xi_n)$}$, und verlange, daß für $ \mbox{$\tilde u(\xi) := u(x(\xi))$}$ eine gewöhnliche Differentialgleichung entsteht. Die transformierte Gleichung lautet nämlich nach der Kettenregel in $ \mbox{$n$}$ Variablen
$ \mbox{$\displaystyle (\tilde \ast)\hspace*{2cm} \sum_{i\in [1,n]} a_i(x) u_{x... ...)_{x_i}\right) + \tilde a_0(\xi) \tilde u(\xi) + \tilde c(\xi) \; =\; 0 \; , $}$
wobei $ \mbox{$\tilde a_i(\xi) := a_i(x(\xi))$}$ und $ \mbox{$\tilde c(\xi) := c(x(\xi))$}$. Setzt man für $ \mbox{$\xi_j$}$ für $ \mbox{$j\in [1,n-1]$}$ (wie oben zu ermittelnde) $ \mbox{$n - 1$}$ unabhängige Lösungen der Rumpfgleichung $ \mbox{$\sum_{i\in [1,n]} a_i(x) u_{x_i} = 0$}$ an, und wird $ \mbox{$\xi_n = x_k$}$ so gewählt, daß auch noch $ \mbox{$\xi_1,\dots,\xi_n$}$ unabhängig sind in dem Sinne, daß die Jacobideterminante
$ \mbox{$\displaystyle \det\left(((\xi_i)_{x_j})_{i,j\in [1,n]}\right) $}$
nicht identisch verschwindet, so wird $ \mbox{$(\tilde \ast)$}$ zur gewöhnlichen Differentialgleichung ersten Grades
$ \mbox{$\displaystyle \tilde a_k(\xi) \tilde u_{\xi_n}(\xi) + \tilde a_0(\xi) \tilde u(\xi) + \tilde c(\xi) \; =\; 0 \; , $}$
in $ \mbox{$\xi_n$}$, mit konstanten Parametern $ \mbox{$\xi_1,\dots,\xi_{n-1}$}$. Die allgemeine Lösung dieser Differentialgleichung ersten Grades ist von der Form
$ \mbox{$\displaystyle \tilde u \; =\; f(\xi_n,c)\; , $}$
$ \mbox{$c$}$ konstant in $ \mbox{$\xi_n$}$, aber in beliebiger Weise abhängig von $ \mbox{$\xi_1,\dots,\xi_{n-1}$}$. Somit erhalten wir als Lösung in den alten Koordinaten
$ \mbox{$\displaystyle u \; =\; f\bigl(x_k,c(\xi_1(x),\dots,\xi_{n-1}(x))\bigr)\; . $}$
Dabei ist $ \mbox{$x = (x_1,\dots,x_n)$}$ abgekürzt, $ \mbox{$\xi_1(x),\dots,\xi_{n-1}(x)$}$ stellt ein System unabhängiger Lösungen der Rumpfdifferentialgleichung dar, und $ \mbox{$c$}$ ist eine beliebige (hinreichend stetig differenzierbare) Funktion in $ \mbox{$n - 1$}$ Variablen.

Bemerkung.

Die Überlegungen zur Lösung des allgemeinen Falls kann man sich auch zunutze machen, wenn man nur $ \mbox{$k$}$ unabhängige Lösungen einer gegebenen Rumpfgleichung in $ \mbox{$n$}$ Variablen gefunden hat, $ \mbox{$k < n-1$}$. Substituiert man diese als $ \mbox{$\xi_1,\dots,\xi_k$}$, und ergänzt diese Koordinatentransformation so, daß die Jacobideterminante nicht identisch verschwindet, so stößt man auf eine noch zu lösende Gleichung in $ \mbox{$n - k$}$ Variablen.

Bemerkung.

Findet man eine geeignete Koordinatentransformation, ist aber nicht in der Lage, die Umkehrung anzugeben, so empfiehlt es sich, die Transformation in mehreren Schritten durchzuführen. D.h. in der Praxis, zunächst einmal eine Variable zu substituieren und den Rest zu übernehmen, und in einem zweiten Schritt eine zweite Variable etc.

(Autoren: Künzer/Meister/Nebe)

Beispiele

Aufgaben

  automatisch erstellt am 21.3.2003