Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
Mathematik-Online-Kurs: Partielle Differentialgleichungen - Wärmeleitungsgleichung

Anfangsrandwertproblem für die eindimensionale Wärmeleitungsgleichung

[vorangehende Seite] [nachfolgende Seite] [Gesamtverzeichnis][Seitenübersicht]
Die Lösung der Wärmeleitungsgleichung

$\displaystyle u_t=u_{xx}+f\ ,\quad x\in(0,\pi)\ ,\ t>0 $

für die Anfangs- und Randwerte

$\displaystyle u(x,0)=a(x),\quad u(0,t)=u(\pi,t)=0 $

lässt sich als Sinus-Reihe darstellen:

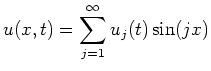
$\displaystyle u(x,t)=\sum_{j=1}^\infty u_j(t)\sin(jx) $

mit

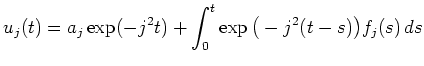
$\displaystyle u_j(t)=a_j\exp(-j^2t) +\int_0^t\exp\big(-j^2(t-s)\big)f_j(s)\,ds $

und

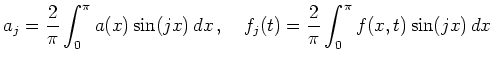
$\displaystyle a_j=\frac{2}{\pi}\int_0^\pi a(x)\sin(jx)\,dx\,,\quad f_j(t)=\frac{2}{\pi}\int_0^\pi f(x,t)\sin(jx)\,dx $

den Sinus-Koeffizienten von $ a$ und $ f(\cdot,t)$.

(Inhalt vorübergehend nicht verfügbar)
Es soll das Wärmeleitungsproblem

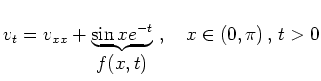
$\displaystyle v_t=v_{xx}+\underbrace{\sin xe^{-t}}_{\displaystyle f(x,t)}\ ,\quad x\in(0,\pi)\,,\,t>0 $

$\displaystyle v(x,0)=0\ ,\quad v(0,t)=0\ ,\quad v(\pi,t)=1 $

gelöst werden.

Aufgrund der inhomogenen Randbedingungen ist zunächst eine Transformation auf Standardform erforderlich. Dazu verwendet man den Ansatz

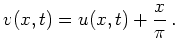
$\displaystyle v(x,t)=u(x,t)+\frac{x}{\pi}\,. $

Dann erfüllt $ u$ dieselbe Differentialgleichung mit den veränderten Anfangs- und Randbedingungen

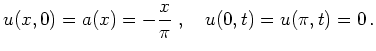
$\displaystyle u(x,0)=a(x)=-\frac{x}{\pi}\ ,\quad u(0,t)=u(\pi,t)=0\,. $

Zur Anwendung der allgemeinen Lösungsformel werden die Sinus-Koeffizienten von $ a$ mit $ f$ berechnet:
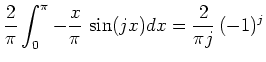$\displaystyle a_j$ $\displaystyle =$ $\displaystyle \frac{2}{\pi}\int_0^\pi-\frac{x}{\pi}\,\sin(jx)dx=\frac{2}{\pi j}\,(-1)^j$  
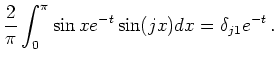$\displaystyle f_j$ $\displaystyle =$ $\displaystyle \frac{2}{\pi}\int_0^\pi\sin xe^{-t}\sin(jx)dx=\delta_{j1}e^{-t}\,.$  

Für $ j=1$ ist $ f_1(s)=e^{-s}$ und

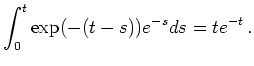
$\displaystyle \int_0^t\exp(-(t-s))e^{-s}ds=te^{-t}\,. $

Somit erhält man

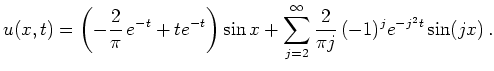
$\displaystyle u(x,t)=\left(-\frac{2}{\pi}\,e^{-t}+te^{-t}\right)\sin x +\sum_{j=2}^\infty\frac{2}{\pi j}\,(-1)^je^{-j^2t}\sin(jx)\,. $

(Autor: Kimmerle)
[vorangehende Seite] [nachfolgende Seite] [Gesamtverzeichnis][Seitenübersicht]
  automatisch erstellt am 5.5.2011