Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
Mathematik-Online-Kurs: MATLAB - Programmierung

for-Schleife

[vorangehende Seite] [nachfolgende Seite] [Gesamtverzeichnis][Seitenübersicht]
Die for-Schleife zur $ n$-fachen Ausführung einer Befehlssequenz besitzt die folgende Syntax:

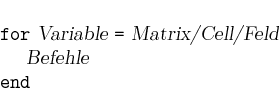
\begin{quote} {\tt for} {\sl Variable} {\tt =} {\sl Matrix/Cell/Feld}\\ \mbox{} \quad {\sl Befehle} \\ {\tt end} \end{quote}

Der Variablen werden nacheinander die Spalten der Matrix bzw. der Cell zugewiesen. Im Falle mehrdimensionaler Felder werden analog die Spalten aller Teilmatrizen durchlaufen. Für jede Spalte werden die Befehle einmal ausgeführt.

Ein $ n$-facher Schleifendurchlauf kann mittels for zaehler=1:n realisiert werden. Im Gegensatz dazu wird der Rumpf der Schleife for zaehler=[1:n]' nur einmal durchlaufen, da es sich bei [1:n]' um einen Spaltenvektor handelt.

Ein vorzeitiger Abbruch der Schleife ist durch Angabe des Befehls break möglich (z.B. innerhalb einer if-Abfrage). Hingegen bewirkt der Befehl continue, dass unmittelbar die nächste Iteration der Schlefe begonnen wird.

Oft können for-Schleifen durch geeignete Vektor-/Matrixoperationen ersetzt werden. Diese sind in der Regel wesentlich effizienter.

(Autoren: Hörner/Wipper)
Mit Hilfe eines Monte-Carlo-Verfahrens soll eine Näherung der Kreiszahl $ \pi\approx 3.1416$ berechnet werden. Hierzu werden $ n$ Zufallspunkte in $ [0,1]^2$ bestimmt. Bezeichnet $ z$ die Anzahl jener Zufallspunkte $ p=(p_1,p_2)$, die in dem Viertelkreises $ p_1^2+p_2^2<1$ liegen, so erhält man für hinreichend große $ n$ die Näherung $ \pi\approx 4z/n$. Der Faktor $ 4$ ergibt sich aus der Tatsache, dass aus Symmetriegründen nur ein Viertelkreis betrachtet wird.

Nachfolgend werden drei unterschiedliche Implementierungen angegeben, deren Laufzeit mit Hilfe der Befehle tic (Start einer Stoppuhr) und toc (Anhalten der Stoppuhr) gemessen wird:

Implementierung mit einer for-Schleife über die Anzahl der Tests: 

  tic
  n=10^6;
  z=0;
  for k=1:n
    p=rand(2,1);
    z=z+(p(1).^2+p(2).^2<1);
  end
  pi=4*z/n
  toc
Ausgabe: 
  pi =
      3.1432
  Elapsed time is 18.367863 seconds.
Die Schleife wird $ n=10^6$ mal durchlaufen. Dabei wird jeweils ein Zufallspunkt generiert und $ z$ um 1 erhöht, sofern dessen quadrierter Betrag kleiner als 1 ist.


Implementierung mit einer for-Schleife über die Spalten einer Zufallspunktematrix: 

  tic
  n=10^6;
  z=0;
  for p=rand(2,n)
    z=z+(p(1).^2+p(2).^2<1);
  end
  pi=4*z/n
  toc
Ausgabe: 
  pi =
      3.1453
  Elapsed time is 11.304552 seconds.
Im Gegensatz zur ersten Implementierung werden alle $ 10^6$ Zufallspunkte mit einem Aufruf der Funktion rand generiert. Die zugehörigen Spaltenvektoren werden anschließend innerhalb der for-Schleife abgearbeitet. Hieraus ergibt sich eine deutliche Laufzeitverkürzung.


Implementierung ohne eine for-Schleife: 

  tic
  n=10^6;
  P=rand(2,n);
  z=sum(P(1,:).^2+P(2,:).^2<1);
  pi=4*z/n
  toc
Ausgabe: 
  pi =
      3.1403
  Elapsed time is 0.388576 seconds.
Zunächst wird eine $ (2\times 10^6)$-Matrix P erstellt, deren Spalten die Zufallspunkte enthalten. Mittels P(1,:).^2+P(2,:).^2 wird ein Vektor bestimmt, welcher die quadrierten Abstände dieser Punkte vom Ursprung enthält. Der Vergleich dieses Vektors mittels <1 ergibt einen logischen Vektor, der bei Summation mittels sum die Anzahl $ l$ ergibt. Diese Implementierung ist um den Faktor 47 bzw. 29 schneller als die beiden Varianten mit for-Schleifen.

(Autoren: Hörner/Wipper)
[vorangehende Seite] [nachfolgende Seite] [Gesamtverzeichnis][Seitenübersicht]
  automatisch erstellt am 5.2.2008