Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
Mathematik-Online-Kurs: Mathematik II für Informatik und Softwaretechnik - Lösungen - Übungsblatt 6

Blatt 6, Aufgabe 4

[vorangehende Seite] [nachfolgende Seite] [Gesamtverzeichnis][Seitenübersicht]

  1. $\displaystyle y\e^{-\frac{z^2}{x^2}} $

    ist stetig ausserhalb $ x_0=0$ als Komposition von stetigen Abbildungen.

    Sei im Weiteren also $ x_0=0$. Untersuchen wir nun den Fall $ z_0=0$. für $ x=\lambda z$ ist die Funktion im Limes $ x,z\to0$ gleich

    $\displaystyle y\e^{-\lambda^2} $

    und dieser hängt damit für $ y\neq0$ von $ \lambda$ ab, und die Funktion kann somit nicht stetig sein. (da sonst natürlich alle Grenzwerte identisch sein müssten.) Da

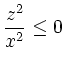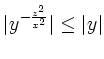
    $\displaystyle \frac{z^2}{x^2}\leq 0$    ist $\displaystyle \vert y\e^{-\frac{z^2}{x^2}}\vert \leq \vert y\vert $

    und damit ist die Funktion stetig in $ x_0=y_0=z_0=0$.

    Im Fall $ z_0\neq 0$ gilt für alle $ (x,y,z)$ in einer Umgebung von $ (0,y_0,z_0)$ $ z^2>c^2$, $ \vert y\vert\leq d$, und somit

    $\displaystyle \vert y\e^{-\frac{z^2}{x^2}}\vert\leq d \left(\e^{-x^{-2}}\right)^{c^2} $

    Aus $ x^2\leq -\frac1{\ln \epsilon}$ folgt $ \e^{-x^{-2}}\leq \epsilon$ und somit ist die Funktion hier stetig

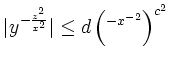
    Insgesammt ist die Funktion also stetig auf der Menge

    $\displaystyle \{(x,y,z)\vert x\neq 0 \lor (x=0\land z\neq0 ) \lor (x=0\land z=0\land y=0)\} $

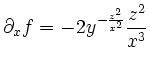
    $\displaystyle \partial_x f= -2y\e^{-\frac{z^2}{x^2}}\frac{z^2}{x^3} $

    Wiederum ausserhalb $ x_0=0$ stetig. Sei nun $ x_0=0$. Für jeden Punkt $ (0,y_0,0)$ lässt sich eine Folge finden, die gegen diesen Punkt konvergiert aber gleichzeitig $ \vert\partial_x f\vert \to\infty$ gilt. Sei $ x=\lambda z$, $ y=y_0$ falls $ y_0\neq 0$, und $ y=\sqrt x$ sonst. Dann ist

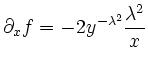
    $\displaystyle \partial_x f= -2y\e^{-\lambda^2}\frac{\lambda^2}{x} $

    also digergent für $ x,z\to0$. Im Fall $ z_0\neq 0$ gilt für alle $ (x,y,z)$ in einer Umgebung von $ (0,y_0,z_0)$ $ d^2>z^2>c^2$, $ \vert y\vert\leq d$, und somit

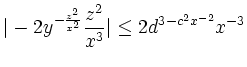
    $\displaystyle \vert-2y\e^{-\frac{z^2}{x^2}}\frac{z^2}{x^3}\vert\leq 2d^3 \e^{-c^2x^{-2}}x^{-3} $

    Wir wollen zeigen, dass es für alle $ \epsilon>0$ ein $ \delta>0$ mit

    $\displaystyle \e^{-c^2x^{-2}}x^{-3} \leq \epsilon$    für alle $\displaystyle \vert x\vert<\delta $

    Äquivalent hierzu ist

    $\displaystyle \e^{-c^2u^{2}}u^{3} \leq \epsilon$    für alle $\displaystyle \vert u\vert>\delta^{-1} $

    Wir überlegen uns zuerst, dass für grosse $ u$ diese Funktion monoton fallend ist (erste Ableitung

    $\displaystyle -c^22u\e^{-c^2u^{2}}u^{3} + 3u^2\e^{-c^2u^{2}} <0$    für $\displaystyle u»1 $

    kleiner null). Danach gilt mit L'Hospital

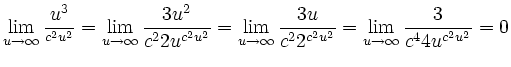
    $\displaystyle \lim_{u\to\infty} \frac{u^3}{\e^{c^2u^{2}}} = \lim_{u\to\infty} \... ...rac{3u}{c^22\e^{c^2u^{2}}} = \lim_{u\to\infty}\frac{3}{c^44u\e^{c^2u^{2}}} = 0 $

    qed. Insgesammt ist die Funktion $ \partial_x f$ also stetig auf der Menge

    $\displaystyle \{(x,y,z)\vert x\neq 0 \lor (x=0\land z\neq0 )\} $

    Für die anderen partiellen Ableitungen gilt

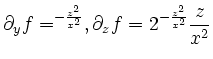
    $\displaystyle \partial_y f= \e^{-\frac{z^2}{x^2}}, \partial_z f= 2\e^{-\frac{z^2}{x^2}}\frac{z}{x^2} $

    und es gelten die obigen Betrachtungen analog

    Insgesammt ist die Funktion also total diffenzierbar auf der Menge

    $\displaystyle \{(x,y,z)\vert x\neq 0 \lor (x=0\land z\neq0 )\} $

  2. Die Funktion

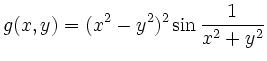
    $\displaystyle g(x,y) = (x^2-y^2)^2\sin\frac{1}{x^2+y^2} $

    ist als Komposition stetiger Funktionen ausserhalb des Nullpunkts stetig. Es gilt

    $\displaystyle \vert g(x,y)\vert \leq (x^2-y^2)^2 $

    und somit ist $ g$ auch bei Null stetig.

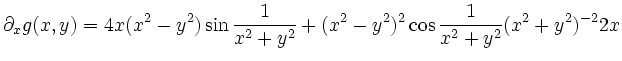
    $\displaystyle \partial_x g(x,y) = 4x(x^2-y^2)\sin\frac{1}{x^2+y^2} + (x^2-y^2)^2\cos\frac{1}{x^2+y^2} (x^2+y^2)^{-2}2x $

    Der erste Term ist wie oben stetig. Für den zweiten gilt

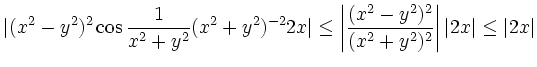
    $\displaystyle \vert(x^2-y^2)^2\cos\frac{1}{x^2+y^2} (x^2+y^2)^{-2}2x\vert\leq \... ...\frac{(x^2-y^2)^2}{(x^2+y^2)^{2}}\right\vert \vert 2x\vert \leq \vert 2x\vert $

    und somit ist auch dieser stetig in Null und damit als Komposition stetiger Funktionen stetig. Die Funktion ist also überall stetig und total differenzierbar.

(Prof. Dr. Eberhard Teufel, Dr. Norbert Röhrl)
[vorangehende Seite] [nachfolgende Seite] [Gesamtverzeichnis][Seitenübersicht]
  automatisch erstellt am 28.10.2006