Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
Mathematik-Online-Kurs: Integralrechnung - Bestimmtes und unbestimmtes Integral

Riemann-Integral

[vorangehende Seite] [nachfolgende Seite] [Gesamtverzeichnis][Seitenübersicht]
Das bestimmte Integral einer stückweise stetigen Funktion $ f$ ist durch

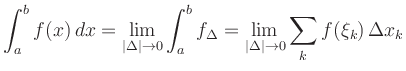
$\displaystyle \int_a^b f(x)\,dx = \lim_{\vert\Delta\vert\to0} \int_a^b f_\Delta = \lim_{\vert\Delta\vert\to0} \sum_{k} f(\xi_k)\,\Delta x_k $

definiert. Dabei bezeichnet $ \Delta:\,a=x_0<x_1<\cdots<x_n=b$ eine Zerlegung von $ [a,b]$,

$\displaystyle \vert\Delta\vert=\max_k \Delta x_k\,, \qquad \Delta x_k=x_k-x_{k-1}\,, $

ist die maximale Intervallänge und $ \xi_k$ ein beliebiger Punkt im $ k$-ten Intervall. Die Summen auf der rechten Seite der Integraldefinition werden Riemann-Summen genannt.

\includegraphics[width=0.6\linewidth]{riemann_bild}

Für positives $ f$ entspricht $ \int_a^b f(x)\,dx$ dem Inhalt der Fläche unterhalb dem Graphen von $ f$.

Es wird die Konvergenz der Riemann-Summen für stetig differenzierbares $ f$ mit Hilfe des Cauchy-Kriteriums gezeigt.

Für eine Folge $ (\Delta_i)$ von Zerlegungen mit $ \vert\Delta_i\vert\to 0$ betrachtet man zwei Folgenglieder $ \Delta_m$ und $ \Delta_n$ und vergleicht die Riemann-Summen mit Hilfe einer Zerlegung $ \Delta$ bestehend aus der Vereinigung der Unterteilungspunkte von $ \Delta_m$ und $ \Delta_n$:

$\displaystyle \Delta_m: x_0<\cdots<x_{k_m},\, \Delta_n: y_0<\cdots<y_{k_n} \quad\leadsto\quad \Delta: z_0<\cdots<z_k \,. $

Die Differenz der Riemann-Summe für $ \Delta$,

$\displaystyle \sum_{j=1}^k f(\zeta_j)\,\Delta z_j,\quad \zeta_i\in[z_{i-1},z_i] \,, $

zu der Riemann-Summe für $ \Delta_m$ kann mit Hilfe des Mittelwertsatzes,

$\displaystyle \vert f(t_1)-f(t_2)\vert \le (t_2-t_1) \max_{t\in [t_1,t_2]} \vert f^\prime(t)\vert \,, $

abgeschätzt werden:
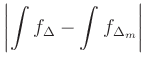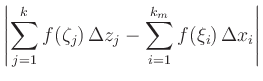$\displaystyle \left\vert\int f_\Delta- \int f_{\Delta_m}\right\vert$ $\displaystyle =$ $\displaystyle \left\vert \sum_{j=1}^{k} f(\zeta_j)\,\Delta z_j - \sum_{i=1}^{k_m} f(\xi_i)\,\Delta x_i\right\vert$  
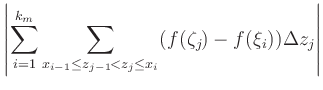  $\displaystyle =$ $\displaystyle \left\vert \sum_{i=1}^{k_m} \sum_{x_{i-1}\le z_{j-1}<z_{j}\le x_{i}} (f(\zeta_j)-f(\xi_i))\Delta z_j\right\vert$  
  $\displaystyle \leq$ $\displaystyle \vert\Delta_m\vert\, \underbrace{\max_{t\in[a,b]} \vert f^\prime(... ...um_{i=1}^{k_m} \sum_{x_{i-1}\le z_{j-1}<z_{j}\le x_{i}} \Delta z_j }_{=b-a} \,,$  

d.h.

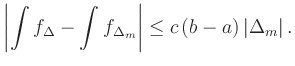
$\displaystyle \left\vert\int f_\Delta- \int f_{\Delta_m}\right\vert \le c\,(b-a)\,\vert\Delta_m\vert \,. $

Mit einer analogen Abschätzung für $ \vert\int f_\Delta-\int f_{\Delta_n}\vert$ folgt die Gültigkeit des Cauchy-Kriteriums:

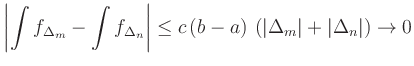$\displaystyle \left\vert\int f_{\Delta_m}-\int f_{\Delta_n}\right\vert \le c\,(b-a)\,\left(\vert\Delta_m\vert+\vert\Delta_n\vert\right)\to 0$   für$\displaystyle \quad m,n\to\infty \,. $

Die Konvergenz zweier Folgen gegen den gleichen Grenzwert lässt sich ähnlich zeigen.

Der technisch etwas schwierigere Beweis für stückweise stetiges $ f$ benutzt die gleichmäßige Stetigkeit:

$\displaystyle \left\vert f(x_1)-f(x_2)\right\vert\leq\varepsilon$   für$\displaystyle \quad \vert x_1-x_2\vert<\delta \,. $

Zur Berechnung von $ \int_0^1 x^2\,dx$ mit Riemann-Summen wird die Folge von Partitionen

$\displaystyle \Delta_n: x_i= i/n,\quad i=0,\ldots,n \,, $

mit den Auswertungsstellen

$\displaystyle \xi_i=(2i-1)/(2n),\quad i=1,\ldots,n \,, $

gewählt.

Die Riemann-Summen sind dann

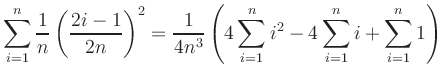$\displaystyle \int f_{\Delta_n}$ $\displaystyle =$ $\displaystyle \sum_{i=1}^n \frac{1}{n}\left(\frac{2i-1}{2n}\right)^2 = \frac{1}{4n^3} \left(4\sum_{i=1}^n i^2-4 \sum_{i=1}^n i + \sum_{i=1}^n 1\right)$  
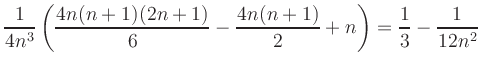  $\displaystyle =$ $\displaystyle \frac{1}{4n^3} \left( \frac{4n(n+1)(2n+1)}{6} - \frac{4n(n+1)}{2} +n \right) = \frac{1}{3} -\frac{1}{12n^2}$  

mit dem Grenzwert

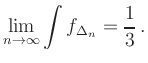
$\displaystyle \lim_{n\to\infty} \int f_{\Delta_n} = \frac{1}{3} \,. $

[vorangehende Seite] [nachfolgende Seite] [Gesamtverzeichnis][Seitenübersicht]
  automatisch erstellt am 5.1.2017