Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
Mathematik-Online-Kurs: Integralrechnung - Uneigentliche Integrale

Gamma-Funktion

[vorangehende Seite] [nachfolgende Seite] [Gesamtverzeichnis][Seitenübersicht]
Die durch

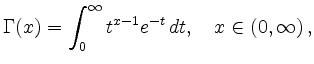
$\displaystyle \Gamma(x) = \int_0^\infty t^{x-1}e^{-t}\,dt, \quad x\in(0,\infty)\, , $

definierte Gamma-Funktion erfüllt die Funktionalgleichung

$\displaystyle \Gamma(x+1) = x\Gamma(x)\, . $

Insbesondere ist $ \Gamma(n+1)=n!$ , $ n\in\mathbb{N}$ .

\includegraphics[width=0.6\linewidth]{gamma.eps}

Mit Hilfe der Funktionalgleichung läß sich die Gamma-Funktion auch für negative Argumente definieren. Wie aus dem abgebildeten Funktionengraphen ersichtlich, besitzt sie einfache Pole für $ x=0,-1,\ldots$ .

(Inhalt vorübergehend nicht verfügbar)
[vorangehende Seite] [nachfolgende Seite] [Gesamtverzeichnis][Seitenübersicht]
  automatisch erstellt am 5.1.2017