Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen] Englische Flagge
Mathematik-Online-Kurs: Vorkurs Mathematik - Analysis - Integralrechnung

Partielle Integration

[vorangehende Seite] [nachfolgende Seite] [Gesamtverzeichnis][Seitenübersicht]
Aus der Produktregel $ (fg)'=f'g+fg'$ ergibt sich eine analoge Formel für unbestimmte Integrale:

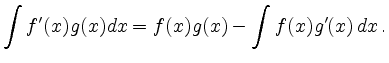
$\displaystyle \int f'(x)g(x)dx=f(x)g(x)- \int f(x)g'(x)\,dx \,. $

Entsprechend gilt

$\displaystyle \int_a^b f'g = \left[ fg \right]_a^b - \int_a^b fg' $

für bestimmte Integrale. Dabei ist zu beachten, dass der Randterm $ \left[ fg \right]_a^b$ verschwindet, wenn eine der beiden Funktionen an den Intervallendpunkten Null ist. Er entfällt ebenfalls für periodische Funktionen mit Periodenlänge $ \left( b-a\right)$.
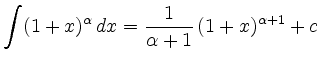Aus $ {\displaystyle{\int (1+x)^\alpha\, dx=\frac{1}{\alpha+1}\,(1+x)^{\alpha+1}+c}}$ für $ \alpha\neq -1$ folgt
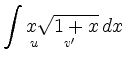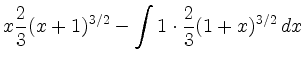$\displaystyle \int \underset{u \quad\:\: v'\quad}{x\sqrt{1+x}}\,dx$ $\displaystyle =$ $\displaystyle x\frac{2}{3}(x+1)^{3/2} - \int 1\cdot\frac{2}{3}(1+x)^{3/2}\,dx$  
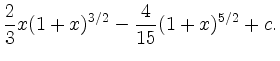  $\displaystyle =$ $\displaystyle \frac{2}{3}x(1+x)^{3/2} - \frac{4}{15}(1+x)^{5/2} + c.$  

Analog berechnet man
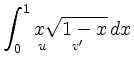$\displaystyle \int_0^1 \underset{u \quad \:\: v'\quad}{x\sqrt{1-x}}\,dx$ $\displaystyle =$ $\displaystyle \left[ -x\frac{2}{3}(1-x)^{3/2} \right]_0^1 + \int_0^1 1\cdot\frac{2}{3}(1-x)^{3/2}\,dx$  
  $\displaystyle =$ $\displaystyle 0 - \left[ \frac{4}{15} (1-x)^{5/2} \right]_0^1 = \frac{4}{15}\,.$  

(Autoren: Höllig/Kopf)
[vorangehende Seite] [nachfolgende Seite] [Gesamtverzeichnis][Seitenübersicht]
  automatisch erstellt am 23.10.2009