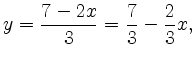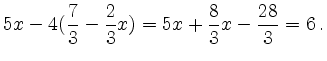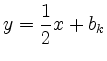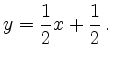Ein lineares Gleichungssystem mit zwei Unbekannten 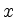 und
und 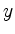 hat die
Form
wobei in jeder Gleichung mindestens einer der Koeffizienten
hat die
Form
wobei in jeder Gleichung mindestens einer der Koeffizienten 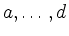 ungleich Null ist.
Es ist genau dann für alle rechten Seiten
ungleich Null ist.
Es ist genau dann für alle rechten Seiten 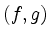 eindeutig lösbar, wenn
eindeutig lösbar, wenn
Die Lösung
lässt sich als Schnittpunkt der durch die beiden Gleichungen beschriebenen
Geraden interpretieren.
Ist 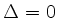 , so sind die Geraden parallel. In diesem Fall existiert
entweder keine Lösung oder, wenn die Geraden zusammenfallen, unendlich viele
Lösungen.
, so sind die Geraden parallel. In diesem Fall existiert
entweder keine Lösung oder, wenn die Geraden zusammenfallen, unendlich viele
Lösungen.
Multipliziert man die erste Gleichung mit 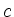 und die zweite mit
und die zweite mit 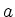 , so folgt
Nach Subtraktion ist
und man erhält die gewünschte Formel für
, so folgt
Nach Subtraktion ist
und man erhält die gewünschte Formel für 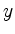 . Die Formel für
. Die Formel für 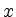 beweist man analog.
beweist man analog.
Für
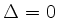 gilt
gilt
mit einem
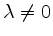 . In diesem Fall haben die Geraden die gleiche Steigung, sind also parallel. Jenachdem, ob
. In diesem Fall haben die Geraden die gleiche Steigung, sind also parallel. Jenachdem, ob 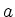 oder
oder 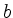 ungleich
Null ist, kann
ungleich
Null ist, kann
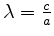 oder
oder
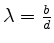 gesetzt werden. Offensichtlich kann das Gleichungssystem nur dann
Lösungen besitzen, wenn
gesetzt werden. Offensichtlich kann das Gleichungssystem nur dann
Lösungen besitzen, wenn
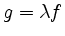 , d.h. wenn die Geraden identisch sind.
, d.h. wenn die Geraden identisch sind.
(Autoren: Höllig/Kreitz)
Als Beispiel wird das Gleichungssystem
betrachtet. Mit
erhält man
Alternativ kann man auch die erste Gleichung nach 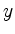 auflösen,
auflösen,
und in die zweite einsetzen:
Damit folgt ebenfalls
und aus der ersten Gleichung 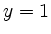 .
.
(Autoren: Höllig/Kreitz)
Als Beispiel wird das Gleichungssystem
mit einem Parameter 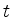 betrachtet.
betrachtet.
Da
sind die den Gleichungen entsprechenden Geraden parallel:
mit
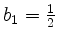 und
und
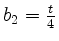 .
Lösungen existieren nur dann, wenn die zweite Gleichung ein Vielfaches der ersten ist, also falls
In diesem Fall sind die Gleichungen äquivalent, es muss also nur eine gelöst werden. Wählt man die erste Gleichung, so kann
.
Lösungen existieren nur dann, wenn die zweite Gleichung ein Vielfaches der ersten ist, also falls
In diesem Fall sind die Gleichungen äquivalent, es muss also nur eine gelöst werden. Wählt man die erste Gleichung, so kann 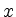 beliebig
gewählt werden und
Die Lösungsmenge ist also eine Gerade durch
beliebig
gewählt werden und
Die Lösungsmenge ist also eine Gerade durch
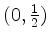 mit Steigung
mit Steigung
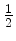 .
.
(Autoren: Höllig/Kreitz)
| |
automatisch erstellt
am 23.10.2009 |




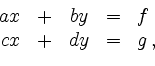
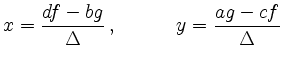
![\includegraphics[width=6cm]{lgsgeraden}](/inhalt/aussage/aussage1275/img8.png)
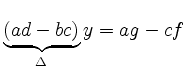
![]() gilt
gilt
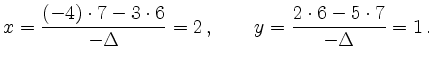
![]() auflösen,
auflösen,