Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen] Englische Flagge
Mathematik-Online-Kurs: Vorkurs Mathematik - Lineare Algebra und Geometrie - Vektorräume

Basis

[vorangehende Seite] [nachfolgende Seite] [Gesamtverzeichnis][Seitenübersicht]
Eine Teilmenge $ B$ eines Vektorraumes $ V$ heißt eine Basis von $ V$, wenn $ B$ linear unabhängig und ein Erzeugendensystem von $ V$ ist, d.h. wenn jeder Vektor $ v\in V$ eine eindeutige Darstellung als endliche Linearkombination

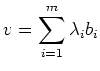
$\displaystyle v = \sum_{i=1}^m \lambda_i b_i $

mit $ b_i\in B$ besitzt.

Ist $ B$ endlich $ (\vert B \vert = n)$, so lässt sich jeder Vektor durch seine Koordinaten bzgl. der Basis beschreiben:

$\displaystyle v \leftrightarrow v_B = (\lambda_1,\ldots,\lambda_n)^{\operatorname t}\,. $

Durch die Koordinatendarstellung

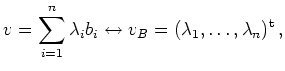
$\displaystyle v = \sum_{i=1}^n \lambda_i b_i \leftrightarrow v_B = (\lambda_1,\ldots,\lambda_n)^{\operatorname t}\, , $

den so genannten kanonischen Isomorphismus, kann man einen endlich dimensionalen $ K$-Vektorraum $ V$ mit dem Vektorraum $ K^n$ der $ n$-Tupel identifizieren. Insbesondere kann man sich also beim Studium reeller und komplexer Vektorräume mit endlicher Basis auf die Prototypen $ \mathbb{R}^n$ und $ \mathbb{C}^n$ beschränken.

Wie man am Beispiel des Vektorraums der Polynome sieht, muss ein Vektorraum keine endliche Basis besitzen. Es werden jedoch im Rahmen der linearen Algebra nur endliche Linearkombinationen betrachtet. Dies impliziert, dass die Folgen

$\displaystyle e_1 = (1,0,0,\ldots)^{\operatorname t},\, e_2 = (0,1,0,\ldots)^{\operatorname t},\, \ldots $

keine Basis für den Vektorraum der Folgen bilden. Das Betrachten unendlicher Linearkombinationen, wie sie etwa in Fourier-Reihen auftreten, liegt auf der Hand, erfordert jedoch einen Konvergenzbegriff, also mehr als nur die bloße Vektorraumstruktur.
(Autoren: App/Höllig)
[vorangehende Seite] [nachfolgende Seite] [Gesamtverzeichnis][Seitenübersicht]
  automatisch erstellt am 23.10.2009