Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen] Englische Flagge
Mathematik-Online-Kurs: Vorkurs Mathematik - Lineare Algebra und Geometrie - Vektoren

Kreuzprodukt

[vorangehende Seite] [nachfolgende Seite] [Gesamtverzeichnis][Seitenübersicht]
Der Vektor

$\displaystyle \vec{c} = \vec{a} \times \vec{b} $

ist zu $ \vec{a}$ und $ \vec{b}$ orthogonal, gemäß der ,,Rechten-Hand-Regel`` orientiert und hat die Länge

$\displaystyle \bigl\vert\vec{c}\bigr\vert = \bigl\vert\vec{a}\bigr\vert\bigl\vert\vec{b}\bigr\vert\sin(\sphericalangle(\vec{a},\vec{b})) \,, $

die dem Flächeninhalt des von den Vektoren $ \vec{a}$ und $ \vec{b}$ aufgespannten Parallelogramms entspricht.
\includegraphics[width=0.6\linewidth]{vektorprodukt.eps}

Insbesondere gilt $ \vec{a} \times \vec{b} = \vec{0}$ für $ \vec{a} \Vert \vec{b}$ und $ \bigl\vert\vec{a}\times\vec{b}\bigr\vert =\bigl\vert\vec{a}\bigr\vert\bigl\vert\vec{b}\bigr\vert$ für $ \vec{a}\bot\vec{b}$.

Alternativ lässt sich das Vektorprodukt durch

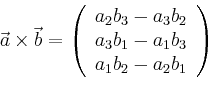
\begin{displaymath} \vec{a}\times\vec{b}=\left( \begin{array}{c} a_2 b_3 - a_... ..._3 b_1 - a_1 b_3 \\ a_1 b_2 - a_2 b_1 \end{array} \right) \end{displaymath}

definieren.
Als Beispiel wird das Kreuzprodukt der Vektoren

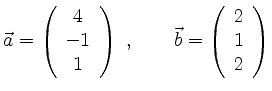
$\displaystyle \vec{a} = \left( \begin{array}{c} 4 \\ -1 \\ 1 \end{array} \right) \ , \qquad \vec{b} = \left( \begin{array}{c} 2 \\ 1 \\ 2 \end{array} \right) $

berechnet. Man erhält

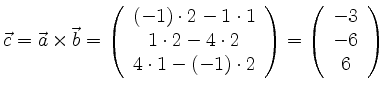
$\displaystyle \vec{c} = \vec{a} \times \vec{b} = \left( \begin{array}{c} (-1) \... ...\end{array} \right) = \left( \begin{array}{c} -3 \\ -6 \\ 6\end{array} \right) $

Bildet man die Beträge, so lässt sich mit der alternativen Definition des Kreuzproduktes der Winkel zwischen den Vektoren bestimmen:

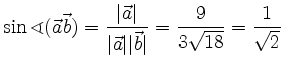
$\displaystyle \sin \sphericalangle (\vec{a} \vec{b} ) = \frac{\vert \vec{a} \ve... ...ert\vec{a}\vert \vert\vec{b}\vert} = \frac{9}{3\sqrt{18}} = \frac{1}{\sqrt{2}} $

impliziert $ \sphericalangle (\vec{a} \vec{b}) = \frac{\pi}{4}$.
(Autoren: Höllig/Kreitz)
[vorangehende Seite] [nachfolgende Seite] [Gesamtverzeichnis][Seitenübersicht]
  automatisch erstellt am 23.10.2009