Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen] Englische Flagge
Mathematik-Online-Kurs: Vorkurs Mathematik - Lineare Algebra und Geometrie - Geraden und Ebenen

Schnitt zweier Ebenen

[vorangehende Seite] [nachfolgende Seite] [Gesamtverzeichnis][Seitenübersicht]
Der kleinere der beiden Winkel $ \varphi\in[0,\pi/2]$ zwischen zwei Ebenen mit Normalenvektoren $ \vec{n}_i$ ist durch

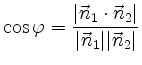
$\displaystyle \cos \varphi = \frac{\vert\vec{n}_1\cdot \vec{n}_2\vert} {\vert\vec{n}_1\vert\vert \vec{n}_2\vert} $

eindeutig bestimmt und

$\displaystyle \vec{u} = \vec{n}_1\times\vec{n}_2 $

ist die Richtung der Schnittgeraden $ g$ . Einen Punkt $ P$ auf $ g$ kann man durch Schnitt mit einer der Koordinatenebenen bestimmen und erhält dann
$ g: \vec{x} = \vec{p} + t\vec{u}$ ,      $ t \in \mathbb{R}$ ,
als Parameterdarstellung von $ g$ .

\includegraphics[clip,width=.6\linewidth]{schnitt}
Für die zwei Ebenen, die jeweils durch die Punkte $ P_1=( 1,2 ,0)$ , $ P_2=(0,1,3)$ und die Normalenvektoren

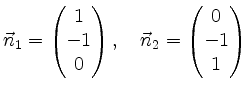
$\displaystyle \vec{n}_1= \begin{pmatrix}1\\ -1\\ 0\\ \end{pmatrix}, \quad \vec{n}_2= \begin{pmatrix}0\\ -1\\ 1\\ \end{pmatrix}$

definiert sind, soll der der Winkel $ \varphi$ zwischen den Ebenen und die Schnittgerade der Ebenen bestimmt werden.


Es ist

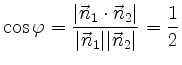
$\displaystyle \cos \varphi = \frac{\vert\vec{n}_1\cdot\vec{n}_2\vert} {\vert\vec{n}_1\vert \vert\vec{n}_2\vert} = \frac{1}{2} $

und damit

$\displaystyle \varphi= \pi/3 \, .$

Weiterhin ist

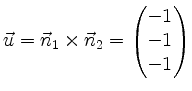
$\displaystyle \vec{u} = \vec{n}_1 \times \vec{n}_2 = \begin{pmatrix}-1\\ -1\\ -1\\ \end{pmatrix}$

die Richtung der Schnittgeraden g. Um einen Punkt $ X$ auf $ g$ zu bestimmen, geht man von den beiden Ebenengleichungen aus:

$\displaystyle E_k: \vec{x}\cdot\vec{n}_k = \vec{p}_k\cdot\vec{n}_k, $

d.h.

$\displaystyle E_1: x_1 - x_2 = -1 $

$\displaystyle E_2: -x_2 + x_3 = 2. $

Wählt man $ x_2$ = 0, ao folgt $ x_1$ = -1 und $ x_3$ = 2. Eine Parameterdarstellung der Schnittgeraden ist somit

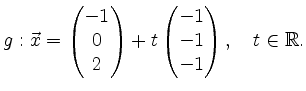
$\displaystyle g: \vec{x} = \begin{pmatrix}-1\\ 0\\ 2\end{pmatrix} + t\begin{pmatrix}-1\\ -1\\ -1\end{pmatrix}, \quad t \in \mathbb{R}. $

(Autoren: Höllig/Weiß )
[vorangehende Seite] [nachfolgende Seite] [Gesamtverzeichnis][Seitenübersicht]
  automatisch erstellt am 23.10.2009