Mathematik-Online-Kurs: Vorkurs Mathematik-Grundlagen-Aussagenlogik-Regeln für logische Operationen

	[Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
	Mathematik-Online-Kurs: Vorkurs Mathematik - Grundlagen - Aussagenlogik
	Regeln für logische Operationen

[vorangehende Seite] [nachfolgende Seite]

[Gesamtverzeichnis][Seitenübersicht]

Für logische Operationen gelten die folgenden Identitäten.

Assoziativgesetze:

$\displaystyle (A\land B)\land C$ $\displaystyle =$ $\displaystyle A \land (B \land C)$

$\displaystyle (A\lor B)\lor C$ $\displaystyle =$ $\displaystyle A \lor (B \lor C)$
Kommutativgesetze:

$\displaystyle A\land B$ $\displaystyle =$ $\displaystyle B \land A$

$\displaystyle A\lor B$ $\displaystyle =$ $\displaystyle B \lor A$
De Morgansche Regeln:

$\displaystyle \lnot(A\land B)$ $\displaystyle =$ $\displaystyle (\lnot A) \lor (\lnot B)$

$\displaystyle \lnot(A\lor B)$ $\displaystyle =$ $\displaystyle (\lnot A) \land (\lnot B)$
Distributivgesetze:

$\displaystyle (A\land B)\lor C$ $\displaystyle =$ $\displaystyle (A\lor C) \land (B\lor C)$

$\displaystyle (A\lor B)\land C$ $\displaystyle =$ $\displaystyle (A\land C) \lor (B\land C)$
Sonstige:

$\displaystyle \lnot(\lnot A)$ $\displaystyle =$ $\displaystyle A$

$\displaystyle A\land A$ $\displaystyle =$ $\displaystyle A$

$\displaystyle A\lor A$ $\displaystyle =$ $\displaystyle A$
Alternative Darstellungen:

$\displaystyle \textrm{Implikation:}\quad$ $\displaystyle A \Rightarrow B$ $\displaystyle \quad =\quad \lnot A \lor B \quad =\quad \lnot A \Leftarrow \lnot B$

$\displaystyle \textrm{Äquivalenz:}\quad$ $\displaystyle A \Leftrightarrow B$ $\displaystyle \quad =\quad (A \land B) \lor (\lnot A \land \lnot B)$

$\displaystyle \textrm{Antivalenz:}\quad$ $\displaystyle A \not\equiv B$ $\displaystyle \quad =\quad (A \land \lnot B) \lor (\lnot A \land B)$

Die alternativen Formulierungen werden oft in Beweisen benutzt.

Ein logischer Ausdruck, der unabhängig vom Wahrheitswert der auftretenden Aussagen immer wahr bzw. immer falsch ist, wird als Tautologie bzw. Kontradiktion bezeichnet. Ein solcher Ausdruck kann bei einer Umformung durch w (oder ) bzw. f (oder 0) ersetzt werden. Insbesondere gelten die Identitäten:

$\displaystyle A \lor \lnot A = \mathrm{w}$	$\displaystyle \textrm{bzw.}$	$\displaystyle A\land \lnot A = \mathrm{f}\,,$
$\displaystyle A \lor \mathrm{w} = \mathrm{w}$	$\displaystyle \textrm{bzw.}$	$\displaystyle A\land \mathrm{w} = A\,,$
$\displaystyle A \lor \mathrm{f} = A$	$\displaystyle \textrm{bzw.}$	$\displaystyle A\land \mathrm{f} = \mathrm{f}\,.$

Die De Morganschen Regeln und die Distributivgesetze lassen sich zeigen, indem man alle Möglichkeiten für die Wahrheitswerte der Aussagen untersucht. Für die erste De Morgansche Regel ist dies in der folgenden Tabelle illustriert.

		$A\land B$	$\lnot A$	$\lnot B$	$\lnot(A\land B)$ , $(\lnot A)\lor(\lnot B)$
w	w	w	f	f	f
w	f	f	f	w	w
f	w	f	w	f	w
f	f	f	w	w	w

Die äquivalenten Beschreibungen für die Implikation, die Äquivalenz und die Antivalenz folgen unmittelbar aus den Definitionen.

(Autoren: Höllig/Hörner)

Zur Illustration der logischen Regeln wird die Aussage

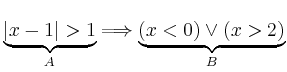
$\displaystyle \underbrace{\vert x-1\vert>1}_{A} \Longrightarrow \underbrace{(x<0)\lor(x>2)}_{B}$

umgeformt.

Anwendung der Morganschen Regel liefert

$\displaystyle \lnot B = \lnot(x<0) \land \lnot(x>2) = (x\ge0)\land(x\le 2) \,.$

Folglich ist die Implikation $A\Rightarrow B$ äquivalent zu der Aussage

$\displaystyle \vert x-1\vert\le1 \Longleftarrow 0\le x\le 2 \,.$

Dieses Ergebnis erhält man auch, indem man die Implikation definitionsgemäß durch

$\displaystyle (\lnot A)\lor B = \vert x-1\vert\le 1 \lor \lnot(0\le x\le 2)$

ersetzt.

(Autoren: Höllig/Hörner)

Als Beispiel wird der Ausdruck

$\displaystyle L: (A \lor B) \Rightarrow (\lnot A \land B)$

vereinfacht. Ersetzen der Implikation und Anwendung der Morgan'schen Regeln ergibt

$\displaystyle \lnot (A \lor B) \lor (\lnot A \land B ) = (\lnot A \land \lnot B) \lor (\lnot A \land B )\,.$

Nach dem Distributivgesetz ist dieser Ausdruck äquivalent zu

$\displaystyle \lnot A \land (\lnot B \lor B) \,.$

Man erkennt, dass der Wahrheitswert von

irrelevant ist und

$\displaystyle L = \lnot A\,.$

Alternativ kann man zur Untersuchung des logischen Ausdrucks auch eine Wahrheitstabelle verwenden.

		$\lnot (A \lor B)$	$\lnot A \land B$
w	w	f	f	f
w	f	f	f	f
f	w	f	w	w
f	f	w	f	w

Es folgt ebenfalls $L = \lnot A$ .

(Autoren: Höllig/Kreitz)

[vorangehende Seite] [nachfolgende Seite]

[Gesamtverzeichnis][Seitenübersicht]

automatisch erstellt am 23.10.2009

$\displaystyle (A\land B)\land C$	$\displaystyle =$	$\displaystyle A \land (B \land C)$
$\displaystyle (A\lor B)\lor C$	$\displaystyle =$	$\displaystyle A \lor (B \lor C)$

$\displaystyle A\land B$	$\displaystyle =$	$\displaystyle B \land A$
$\displaystyle A\lor B$	$\displaystyle =$	$\displaystyle B \lor A$

$\displaystyle \lnot(A\land B)$	$\displaystyle =$	$\displaystyle (\lnot A) \lor (\lnot B)$
$\displaystyle \lnot(A\lor B)$	$\displaystyle =$	$\displaystyle (\lnot A) \land (\lnot B)$

$\displaystyle (A\land B)\lor C$	$\displaystyle =$	$\displaystyle (A\lor C) \land (B\lor C)$
$\displaystyle (A\lor B)\land C$	$\displaystyle =$	$\displaystyle (A\land C) \lor (B\land C)$

$\displaystyle \lnot(\lnot A)$	$\displaystyle =$	$\displaystyle A$
$\displaystyle A\land A$	$\displaystyle =$	$\displaystyle A$
$\displaystyle A\lor A$	$\displaystyle =$	$\displaystyle A$

$\displaystyle \textrm{Implikation:}\quad$	$\displaystyle A \Rightarrow B$	$\displaystyle \quad =\quad \lnot A \lor B \quad =\quad \lnot A \Leftarrow \lnot B$
$\displaystyle \textrm{Äquivalenz:}\quad$	$\displaystyle A \Leftrightarrow B$	$\displaystyle \quad =\quad (A \land B) \lor (\lnot A \land \lnot B)$
$\displaystyle \textrm{Antivalenz:}\quad$	$\displaystyle A \not\equiv B$	$\displaystyle \quad =\quad (A \land \lnot B) \lor (\lnot A \land B)$