Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen] Englische Flagge
Mathematik-Online-Kurs: Vorkurs Mathematik - Analysis - Stetigkeit

Stetigkeit

[vorangehende Seite] [nachfolgende Seite] [Gesamtverzeichnis][Seitenübersicht]
Eine Funktion $ f$ ist stetig im Punkt $ a$, wenn für alle Folgen $ (x_n)$ mit Grenzwert $ a$ die Funktionswerte $ f(x_n)$ gegen $ f(a)$ konvergieren:

$\displaystyle x_n \rightarrow a \Longrightarrow f(x_n) \rightarrow f(a)\,,$

Nach Definition des Grenzwerts gibt es zu jedem $ \varepsilon > 0$ ein $ \delta_{\varepsilon}$ mit

$\displaystyle \vert f(x)-f(a)\vert < \varepsilon$    für $\displaystyle \vert x-a\vert < \delta_{\varepsilon}\,,$

und man schreibt $ \lim\limits_{x\rightarrow a}f(x) = f(a)$.

\includegraphics[width=0.6\linewidth]{Beispiel_Stetigkeit.eps}

Eine Funktion ist stetig auf einem Intervall $ D$, wenn sie in jedem Punkt von $ D$ stetig ist. Dies bedeutet, dass der Graph von $ f$ zusammenhängend ist, die Funktion besitzt keine Sprung- oder Polstellen.

Anschaulich bedeutet Stetigkeit, dass sich der Graph ohne abzusetzen zeichnen lässt.

Die folgenden beiden Beispiele illustrieren verschiedene Typen von Unstetigkeitsstellen.

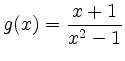
Funktion $ f(x)=\operatorname{sign}(x)$   Funktion $ {\displaystyle{g(x)=\frac{x+1}{x^2-1}}}$
\includegraphics[height=4.5cm]{sign_1.eps}   \includegraphics[height=4.5cm]{hebbare_defluecke.eps}

Die Signum-Funktion $ \operatorname{sign}$ hat an der Stelle Null einen Sprung. Zwar ist ein Funktionswert definiert, $ \operatorname{sign}(0)=0$ , der Grenzwert von $ f(x)$ für $ x \rightarrow 0$ existiert jedoch nicht.

Die Funktion $ g$ hat Definitionslücken bei $ x=\pm 1$ . Für $ x\rightarrow 1$ strebt $ \left\vert g(x)\right\vert$ gegen $ \infty$ , $ g$ hat dort eine Polstelle. Der Grenzwert $ \lim \limits_{x \rightarrow -1} g(x)$ existiert jedoch. Dies sieht man unmittelbar durch Kürzen des Linearfaktors $ (x+1)$ :

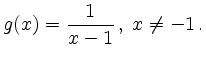
$\displaystyle g(x)=\frac{1}{x-1}\,,\; x \neq -1 \,. $

Es handelt sich um eine hebbare Definitionslücke. Durch Ergänzen des Funktionswertes $ g(-1)=-\frac{1}{2}$ wird $ g$ zu einer auf $ \mathbb{R}\backslash \left\{1\right\}$ stetigen Funktion.

(Autoren: App/Höllig )
[vorangehende Seite] [nachfolgende Seite] [Gesamtverzeichnis][Seitenübersicht]
  automatisch erstellt am 23.10.2009