Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
Mathematik-Online-Kurs: Partielle Differentialgleichungen - Poisson-Gleichung

Eigenfunktionen des Laplace-Operators auf der Einheitskreisscheibe

[vorangehende Seite] [nachfolgende Seite] [Gesamtverzeichnis][Seitenübersicht]

Das Eigenwertproblem

$\displaystyle -\Delta u = \lambda u\ (r<1),\quad u=0\ (r=1), $

auf der Einheitskreisscheibe $ D:\ r=\vert(x_1,x_2)\vert<1$ besitzt die Eigenfunktionen

$\displaystyle u_{k,n}(r,\varphi) = J_{\vert k\vert}(\mu_{\vert k\vert,n}r) e^{\mathrm{i}k\varphi}, \quad k\in\mathbb{Z},\, n\in\mathbb{N}\,, $

mit $ \mu_{\vert k\vert,n}>0$ den Nullstellen der Bessel-Funktion $ J_{\vert k\vert}$. Die entsprechenden Eigenwerte sind $ \lambda_{k,n}=\mu_{\vert k\vert,n}^2$.

Die Funktionen $ u_{k,n}$ bilden ein vollständiges Orthogonalsystem im Raum $ L_2(D)$ der auf $ D$ quadratintegrierbaren Funktionen bzgl. des Skalarproduktes

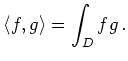
$\displaystyle \langle f,g \rangle = \int_D fg\,. $

Insbesondere besitzt jede Lösung der Poisson-Gleichung $ -\Delta u = f$ die Entwicklung

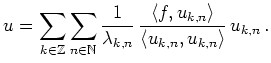
$\displaystyle u = \sum_{k\in\mathbb{Z}}\sum_{n\in\mathbb{N}} \frac{1}{\lambda_... ...rac{\langle f,u_{k,n} \rangle} {\langle u_{k,n},u_{k,n} \rangle}\, u_{k,n} \,. $

(Inhalt vorübergehend nicht verfügbar)
[vorangehende Seite] [nachfolgende Seite] [Gesamtverzeichnis][Seitenübersicht]
  automatisch erstellt am 5.5.2011