Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen] Englische Flagge
Mathematik-Online-Kurs: Vektorrechnung - Ebenen

Abstand Punkt-Ebene

[vorangehende Seite] [nachfolgende Seite] [Gesamtverzeichnis][Seitenübersicht]
Der Lotvektor eines Punktes $ Q$ auf eine Ebene E durch $ P$ mit Normalenvektor $ \vec{n}$ ist

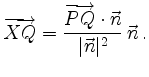
$\displaystyle \overrightarrow{XQ} = \frac{\overrightarrow{PQ}\cdot\vec{n}} {\vert\vec{n}\vert^2}\,\vec{n}\,. $

Seine Länge

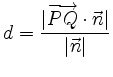
$\displaystyle d = \frac{\vert\overrightarrow{PQ}\cdot\vec{n}\vert} {\vert\vec{n}\vert} $

ist der Abstand der Ebene zu $ Q$ . Der Punkt $ X$ mit Ortsvektor

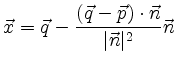
$\displaystyle \vec{x} = \vec{q} - \frac{(\vec{q}-\vec{p})\cdot\vec{n}}{\vert\vec{n}\vert^2} \vec{n} $

wird als Projektion von $ Q$ auf $ E$ bezeichnet.

\includegraphics[width=10cm]{abstand}

(Inhalt vorübergehend nicht verfügbar)
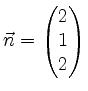Für die Ebene durch den Punkt $ P=(1,2,3)$ mit Normalenvektor $ \vec{n}=\begin{pmatrix}2\\ 1\\ 2\\ \end{pmatrix}$ soll der Abstand $ d$ des Punktes $ Q=(3,2,3)$ sowie die Projektion $ X$ auf die Ebene bestimmt werden.


Zunächst ist

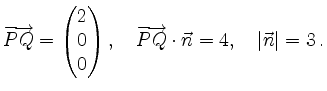
$\displaystyle \overrightarrow{PQ} = \begin{pmatrix}2 \\ 0 \\ 0 \end{pmatrix},\quad \overrightarrow{PQ} \cdot \vec{n} = 4,\quad \vert\vec{n}\vert = 3\, . $

Damit erhält man

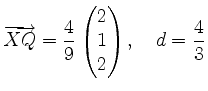
$\displaystyle \overrightarrow{XQ} = \frac{4}{9} \begin{pmatrix}2\\ 1\\ 2\\ \end{pmatrix},\quad d = \frac{4}{3} $

und errechnet schließlich

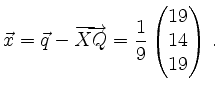
$\displaystyle \vec{x} = \vec{q} - \overrightarrow{XQ} = \frac{1}{9} \begin{pmatrix}19\\ 14\\ 19\\ \end{pmatrix}\, . $

(Autoren: Höllig/Weiß )
[vorangehende Seite] [nachfolgende Seite] [Gesamtverzeichnis][Seitenübersicht]
  automatisch erstellt am 17.3.2011