

Mathematik-Online-Kurs: Vorkurs Mathematik - Lineare Algebra und Geometrie - Vektorräume

|
[Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen] |

|
|
Mathematik-Online-Kurs: Vorkurs Mathematik - Lineare Algebra und Geometrie - Vektorräume | ||
Dimension | ||
| [vorangehende Seite] [nachfolgende Seite] | [Gesamtverzeichnis][Seitenübersicht] |
Besitzt ein Vektorraum ![]() eine endliche Basis
eine endliche Basis
![]() , so ist
die Anzahl der Basisvektoren eindeutig bestimmt und wird als Dimension von
, so ist
die Anzahl der Basisvektoren eindeutig bestimmt und wird als Dimension von ![]() bezeichnet:
bezeichnet:
Man setzt
![]() für
für ![]() und
und
![]() für einen Vektorraum ohne endliche Basis.
für einen Vektorraum ohne endliche Basis.
Nach dem allgemeinen Basissatz besitzt jeder Vektorraum eine Basis.
Hat ein Vektorraum eine ![]() -elementige Basis
-elementige Basis
Würden nämlich zwei Basen mit unterschiedlich vielen Vektoren existieren, erhält man einen Widerspruch zur linearen Unabhängigkeit der Basisvektoren.
Die obige Behauptung kann durch Induktion nach
![]() bewiesen werden.
bewiesen werden.
Für den Induktionsschritt (der Induktionsanfang
![]() ist trivial) betrachtet man die
Basisdarstellung der Vektoren
ist trivial) betrachtet man die
Basisdarstellung der Vektoren ![]() :
:
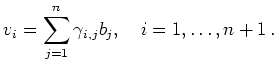 |
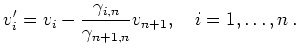
| [vorangehende Seite] [nachfolgende Seite] | [Gesamtverzeichnis][Seitenübersicht] |
| automatisch erstellt am 23.10.2009 |