#./interaufg69.tex#Die Ebene
zerlegt den Tetraeder mit den Eckpunkten
in zwei Teilkörper.
Bestimmen Sie die Kantenschnittpunkte
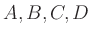 .
Berechnen Sie die Volumina des Tetraeders sowie des Teilkörpers, der den Ursprung
.
Berechnen Sie die Volumina des Tetraeders sowie des Teilkörpers, der den Ursprung 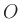 enthält.
enthält.
Hinweis:
Das gestrichelte Dreieck
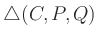 zerlegt einen der Teilkörper in ein Prisma und in eine Pyramide mit viereckiger Grundfläche.
zerlegt einen der Teilkörper in ein Prisma und in eine Pyramide mit viereckiger Grundfläche.
Antwort:
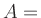 ( , , )
( , , )
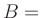 ( , , )
( , , )
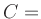 ( , , )
( , , )
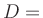 ( , , )
( , , )
 ,
,
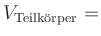
(auf drei Dezimalstellen gerundet)



