
Mathematik-Online-Lexikon:

|
[Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen] |
|
Mathematik-Online-Lexikon: | |
Koordinatenfreie Definition der Rotation |
| A B C D E F G H I J K L M N O P Q R S T U V W X Y Z | Übersicht |
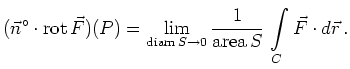
Dabei wird der Grenzwert über eine Folge regulärer Flächen ![]() mit orientiertem Rand
mit orientiertem Rand
![]() gebildet, die alle
den Punkt
gebildet, die alle
den Punkt ![]() enthalten und dort die Normale
enthalten und dort die Normale ![]() haben, wobei der
größte Abstand zweier Flächenpunkte (diam
haben, wobei der
größte Abstand zweier Flächenpunkte (diam ![]() ) und damit auch der Fächeninhalt
gegen null geht.
) und damit auch der Fächeninhalt
gegen null geht.
![\includegraphics[clip=true,width=.4\linewidth]{a_rotation_bild_beschriftung}](/inhalt/aussage/aussage798/img7.png)
Das Skalarprodukt auf der linken Seite wird
als Wirbelstärke von ![]() um
um
![]() bezeichnet
und ist für
bezeichnet
und ist für
![]() am größten.
am größten.
Diese geometrische Charakterisierung der Rotation
folgt unmittelbar aus dem Satz von Stokes
und dem Mittelwertsatz.
Sie zeigt insbesondere, dass
![]() invariant unter orthogonalen
Koordinatentransformationen ist.
invariant unter orthogonalen
Koordinatentransformationen ist.
siehe auch:
| automatisch erstellt am 19. 8. 2013 |