Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
Mathematik-Online-Lexikon:

Berechnung der Jordanform

A B C D E F G H I J K L M N O P Q R S T U V W X Y Z Übersicht

Sei

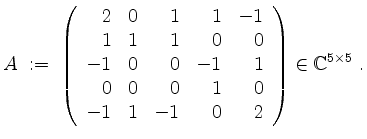
$\displaystyle A \;:=\; \left(\begin{array}{rrrrr} 2 & 0 & 1 & 1 & -1 \\ 1 & 1... ... 0 \\ -1 & 1 & -1 & 0 & 2 \\ \end{array}\right) \in\mathbb{C}^{5\times 5}\;. $

Bestimme so eine invertierbare Matrix $ S$ und eine Matrix $ J$ in Jordanform, daß

$\displaystyle S^{-1}AS \;=\; J\;. $

Lösung.

Das charakteristische Polynom berechnet sich zu

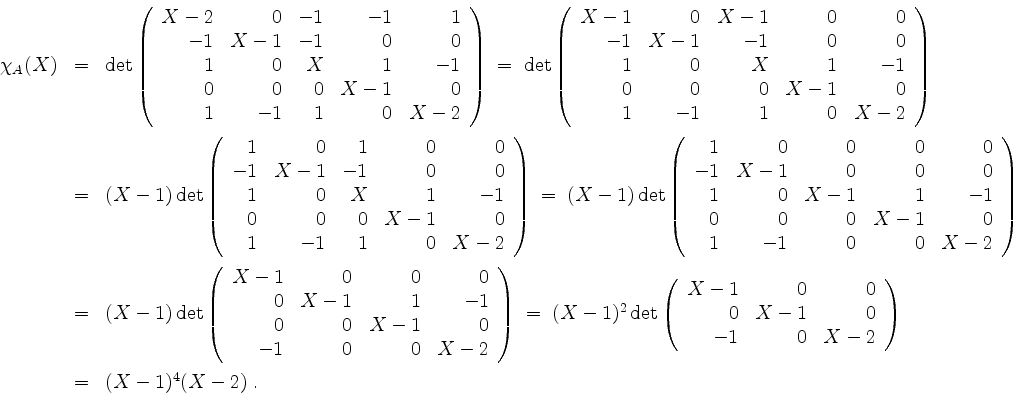
\begin{displaymath} \begin{array}{rcl} \chi_A(X) & = & \det\left(\begin{array}... ...\right)\vspace*{2mm}\\ &=& (X-1)^4 (X - 2) \;. \\ \end{array}\end{displaymath}

Wir erhalten so die Eigenwerte $ \lambda_1 = 1$ mit der algebraischen Vielfachheit $ m_1 = 4$ und $ \lambda_2 = 2$ mit der algebraischen Vielfachheit $ m_2 = 1$ .

Im folgenden verwenden wir die formale Schreibweise des Algorithmus.

Beginnen wir mit $ \lambda_2 = 2$ . Es ist hier $ C = A - 2\mathrm{E}$ . Mit der Zeilenstufenform

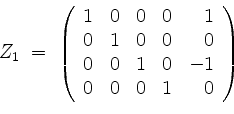
\begin{displaymath} Z_1 \; =\; \left( \begin{array}{rrrrr} 1 & 0 & 0 & 0 & 1 \\ ... ... & 0 & 1 & 0 & -1 \\ 0 & 0 & 0 & 1 & 0 \\ \end{array}\right) \end{displaymath}

von $ C$ erhalten wir

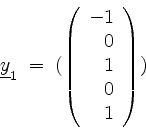
\begin{displaymath} \underline{y}_1 \; = \; ( \left( \begin{array}{r} -1 \\ 0 \\ 1 \\ 0 \\ 1 \\ \end{array}\right) ) \end{displaymath}

als eine Basis von $ \operatorname{Kern}(C^1) = \mathrm{E}_A(2)$ . Da die Dimension dieses Eigenraums gleich der algebraischen Vielfachheit ist, können wir sogleich den gefundenen Vektor $ x_{1,1} = y_{1,1}$ als einzigen Eintrag der Kette $ \mathrm{Kette}(x_{1,1}) = (x_{1,1})$ in die Matrix $ S$ eintragen.

Fahren wir mit $ \lambda_1 = 1$ fort. Es ist hier $ C = A - \mathrm{E}$ . Mit der Zeilenstufenform

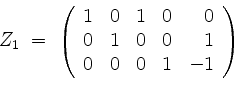
\begin{displaymath} Z_1 \; =\; \left( \begin{array}{rrrrr} 1 & 0 & 1 & 0 & 0 \\ 0 & 1 & 0 & 0 & 1 \\ 0 & 0 & 0 & 1 & -1 \\ \end{array}\right) \end{displaymath}

von $ C$ erhalten wir

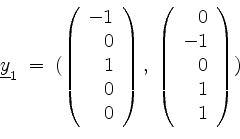
\begin{displaymath} \underline{y}_1 \; = \; ( \left( \begin{array}{r} -1 \\ 0 ... ...ay}{r} 0 \\ -1 \\ 0 \\ 1 \\ 1 \\ \end{array}\right) ) \end{displaymath}

als eine Basis von $ \operatorname{Kern}(C^1)$ . Mit der Zeilenstufenform

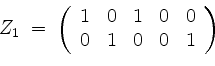
\begin{displaymath} Z_1 \; =\; \left( \begin{array}{rrrrr} 1 & 0 & 1 & 0 & 0 \\ 0 & 1 & 0 & 0 & 1 \\ \end{array}\right) \end{displaymath}

von $ Z_1\cdot C$ (und damit auch von $ C^2$ ) erhalten wir

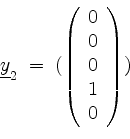
\begin{displaymath} \underline{y}_2 \; = \; ( \left( \begin{array}{r} 0 \\ 0 \\ 0 \\ 1 \\ 0 \\ \end{array}\right) ) \end{displaymath}

als eine Basisergänzung von $ \operatorname{Kern}(C^1)$ zu $ \operatorname{Kern}(C^2)$ . Mit der Zeilenstufenform

\begin{displaymath} Z_3 \; =\; \left( \begin{array}{rrrrr} 0 & 1 & 0 & 0 & 1 \\ \end{array}\right) \end{displaymath}

von $ Z_2\cdot C$ (und damit auch von $ C^3$ ) erhalten wir

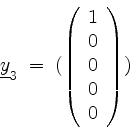
\begin{displaymath} \underline{y}_3 \; = \; ( \left( \begin{array}{r} 1 \\ 0 \\ 0 \\ 0 \\ 0 \\ \end{array}\right) ) \end{displaymath}

als eine Basisergänzung von $ \operatorname{Kern}(C^2)$ zu $ \operatorname{Kern}(C^3) = \mathrm{H}_A(1)$ .

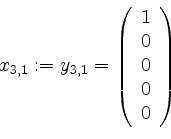In Stufe $ 3$ nehmen wir \begin{displaymath}x_{3,1} := y_{3,1} = \left( \begin{array}{r} 1 \\ 0 \\ 0 \\ 0 \\ 0 \\ \end{array}\right) \end{displaymath} .

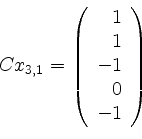In Stufe $ 2$ ist nun zunächst \begin{displaymath}C x_{3,1} = \left( \begin{array}{r} 1 \\ 1 \\ -1 \\ 0 \\ -1 \\ \end{array}\right)\end{displaymath} . Die aus $ \underline{y}_2$ zu treffende Auswahl ist leer.

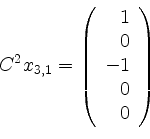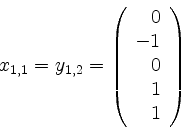In Stufe $ 1$ ist nun zunächst \begin{displaymath}C^2 x_{3,1} = \left( \begin{array}{r} 1 \\ 0 \\ -1 \\ 0 \\ 0 \\ \end{array}\right)\end{displaymath} , so daß wir aus $ \underline{y}_1$ den Vektor \begin{displaymath}x_{1,1} = y_{1,2} = \left( \begin{array}{r} 0 \\ -1 \\ 0 \\ 1 \\ 1 \\ \end{array}\right)\end{displaymath} auswählen können (nicht aber $ y_{1,1}$ !). Tragen wir nun noch die Ketten $ \mathrm{Kette}(x_{3,1}) = (C^2 x_{3,1}, Cx_{3,1}, x_{3,1})$ und $ \mathrm{Kette}(x_{1,1}) = (x_{1,1})$ in die Matrix $ S$ ein.

Wir erhalten

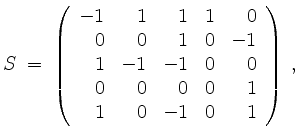
$\displaystyle S \;=\; \left(\begin{array}{rrrrr} -1 & 1 & 1 & 1 & 0 \\ 0 & 0 ... ... 0 & 0 \\ 0 & 0 & 0 & 0 & 1 \\ 1 & 0 & -1 & 0 & 1 \\ \end{array}\right)\; , $

so erhalten wir entsprechend (ohne dafür $ S^{-1}$ berechnen zu müssen)

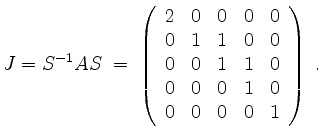
$\displaystyle J = S^{-1} AS \;=\; \left(\begin{array}{rrrrr} 2 & 0 & 0 & 0 & 0... ...& 1 & 0 \\ 0 & 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 & 1 \\ \end{array}\right)\; . $

Zur Probe verifizieren wir stattdessen, daß $ S$ invertierbar ist, und daß $ SJ = AS$ .
(Autoren: Künzer/Martin/Tentler/Wahrheit)
[Verweise]
  automatisch erstellt am 22.  8. 2006