Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
Mathematik-Online-Lexikon:

Extrema mit Nebenbedingungen

A B C D E F G H I J K L M N O P Q R S T U V W X Y Z Übersicht

Sei $ f(x,y) = x^2 + y^2$, und sei $ g(x,y) = 2 x^2 + y^2 - 1$, beide auf ganz $ \mathbb{R}^2$ definiert.

Bestimme die lokalen Extrema von $ f$ unter Nebenbedingung $ g = 0$.

Lösung.

Sei $ f(x,y) = x^2 + y^2$, und sei $ g(x,y) = 2 x^2 + y^2 - 1$, jeweils auf ganz $ \mathbb{R}^2$. Bestimme die lokalen Extrema von $ f$ unter Nebenbedingung $ g = 0$.

Notwendige Bedingung. Wir ermitteln die regulären kritischen Punkte. Mit $ F = f - \lambda g$ ist $ F'(x,y) = \begin{pmatrix}2x - 4\lambda x\; & \; 2y - 2\lambda y\end{pmatrix}$. Zu lösen ist folglich das Gleichungssystem

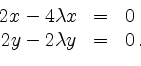
\begin{displaymath} \begin{array}{rcl} 2x - 4\lambda x & = & 0 \\ 2y - 2\lambda y & = & 0\,. \\ \end{array}\end{displaymath}

Im Falle $ x = 0$ erhalten wir aus der Nebenbedingung $ g = 0$, daß $ y = \pm 1$, und schließlich aus der zweiten Gleichung des Gleichungssystems $ \lambda = 1$. Dies liefert die kritischen Punkte $ (0,1)^\mathrm{t}$ und $ (0,-1)^\mathrm{t}$, die in der Tat regulär sind, da dort $ g'\ne 0$ gilt, und also der Rang von $ g'$ gleich $ 1$ ist. An diesen beiden Punkten ist $ \lambda = 1$.

Im Falle $ x\ne 0$ erhalten wir aus der ersten Gleichung des Gleichungssystems, daß $ \lambda = 1/2$, und folglich aus der zweiten Gleichung, daß $ y = 0$, und schließlich aus der Nebenbedingung $ g = 0$, daß $ x = \pm 2^{-1/2}$. Dies liefert die kritischen Punkte $ (2^{-1/2},0)^\mathrm{t}$ und $ (-2^{-1/2},0)^\mathrm{t}$, die in der Tat regulär sind, da dort $ g'\ne 0$ gilt, und also der Rang von $ g'$ gleich $ 1$ ist. An diesen beiden Punkten ist $ \lambda = 1/2$.

Hinreichende Bedingung. Bestimmen wir zunächst für beliebiges $ \lambda\in\mathbb{R}$ die Hessematrix

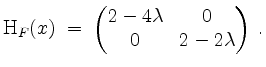
$\displaystyle \mathrm{H}_F(x) \;=\; \begin{pmatrix}2 - 4\lambda&0\\ 0&2 - 2\lambda\end{pmatrix}\; . $

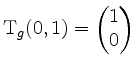Im Punkt $ (0,1)^\mathrm{t}$ ist $ g'(0,1) = \begin{pmatrix}0 & 2\end{pmatrix}$ und $ \lambda = 1$. Also wird z.B. $ \mathrm{T}_g(0,1) = \begin{pmatrix}1 \\ 0\end{pmatrix}$, und folglich

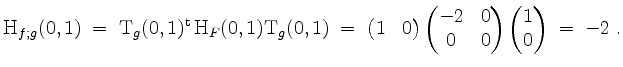
$\displaystyle \mathrm{H}_{f;g}(0,1) \;=\; \mathrm{T}_g(0,1)^\mathrm{t}\, \mathr... ...pmatrix}-2&0\\ 0&0\end{pmatrix}\begin{pmatrix}1 \\ 0\end{pmatrix} \;=\; -2\; . $

Aus deren negativer Definitheit folgt, daß in $ (0,1)^\mathrm{t}$ ein lokales Maximum unter Nebenbedingung $ g = 0$ vorliegt.

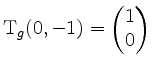Im Punkt $ (0,-1)^\mathrm{t}$ ist $ g'(0,-1) = \begin{pmatrix}0 & -2\end{pmatrix}$ und $ \lambda = 1$. Also wird z.B. $ \mathrm{T}_g(0,-1) = \begin{pmatrix}1 \\ 0\end{pmatrix}$, und folglich

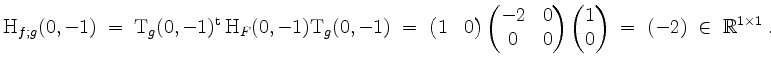
$\displaystyle \mathrm{H}_{f;g}(0,-1) \;=\; \mathrm{T}_g(0,-1)^\mathrm{t}\, \mat... ...begin{pmatrix}1 \\ 0\end{pmatrix} \;=\; (-2) \;\in\;\mathbb{R}^{1\times 1}\; . $

Aus deren negativer Definitheit folgt, daß in $ (0,-1)^\mathrm{t}$ ein lokales Maximum unter Nebenbedingung $ g = 0$ vorliegt.

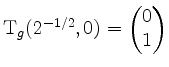Im Punkt $ (2^{-1/2},)^\mathrm{t}$ ist $ g'(2^{-1/2},0) = \begin{pmatrix}\sqrt{8}&0\end{pmatrix}$ und $ \lambda = 1/2$. Also wird z.B. $ \mathrm{T}_g(2^{-1/2},0) = \begin{pmatrix}0 \\ 1\end{pmatrix}$, und folglich

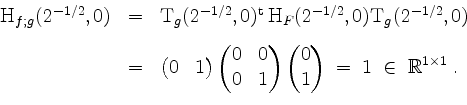
\begin{displaymath} \begin{array}{rcl} \mathrm{H}_{f;g}(2^{-1/2},0) &=& \mathrm{... ...d{pmatrix} \;=\; 1\;\in\;\mathbb{R}^{1\times 1}\; . \end{array}\end{displaymath}

Aus deren positiver Definitheit folgt, daß in $ (2^{-1/2},0)^\mathrm{t}$ ein lokales Minimum unter Nebenbedingung $ g = 0$ vorliegt.

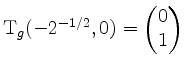Im Punkt $ (-2^{-1/2},)^\mathrm{t}$ ist $ g'(-2^{-1/2},0) = \begin{pmatrix}-\sqrt{8}&0\end{pmatrix}$ und $ \lambda = 1/2$. Also wird z.B. $ \mathrm{T}_g(-2^{-1/2},0) = \begin{pmatrix}0 \\ 1\end{pmatrix}$, und folglich

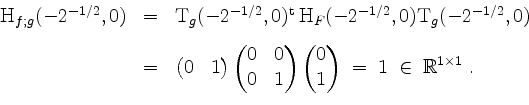
\begin{displaymath} \begin{array}{rcl} \mathrm{H}_{f;g}(-2^{-1/2},0) &=& \mathrm... ...d{pmatrix} \;=\; 1\;\in\;\mathbb{R}^{1\times 1}\; . \end{array}\end{displaymath}

Aus deren positiver Definitheit folgt, daß in $ (-2^{-1/2},0)^\mathrm{t}$ ein lokales Minimum unter Nebenbedingung $ g = 0$ vorliegt.

Als Probe kann man anführen, daß $ f$ an den ersten beiden kritischen Punkten je den Wert $ 1$ annimmt, an den letzten beiden kritischen Punkten je den Wert $ 1/2$. Da $ V(g)$ kompakt ist, müssen sich die beiden globale Extrema unter den lokalen Extrema befinden. Einen Widerspruch hätten wir, wenn wir nun folgern könnten, daß das globale Minimum größer als das globale Maximum sein müßte - was glücklicherweise nicht der Fall ist.

(Autoren: Künzer/Martin/Tentler/Wahrheit)

siehe auch:

  automatisch erstellt am 14.  5. 2007