Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
Mathematik-Online:

Extrema und Extrema mit Nebenbedingungen

A B C D E F G H I J K L M N O P Q R S T U V W X Y Z Übersicht

Lokale Extrema.

Sei $ M\subseteq\mathbb{R}^n$ . Eine Funktion $ f:M\to\mathbb{R}$ besitzt ein lokales Minimum (bzw. lokales Maximum) an der Stelle $ x_0\in M$ , falls es ein $ \varepsilon>0$ gibt, so daß $ f(x_0)\leq f(x)$ (bzw. $ f(x_0)\geq f(x)$ ) für alle $ x\in B_\varepsilon(x_0)\cap M$ .

Die Funktion $ f$ hat an der Stelle $ x_0\in M$ ein lokales Extremum, wenn $ f$ an der Stelle $ x_0$ ein lokales Minimum oder lokales Maximum hat.

Notwendige Bedingung. Sei $ x_0$ ein innerer Punkt von $ M$ , und sei $ f$ partiell differenzierbar in $ x_0$ . Hat $ f$ an der Stelle $ x_0$ ein lokales Extremum, so ist $ \nabla f(x_0)=0$ .

Ein innerer Punkt $ x_0$ von $ M$ , für den $ \nabla f(x_0)=0$ gilt, heißt kritischer Punkt. Ein kritischer Punkt ist also ein Kandidat für eine lokale Extremstelle.

Hinreichende Bedingung. Sei $ x_0$ ein innerer Punkt von $ M$ , und sei $ f$ zweimal stetig differenzierbar in einer Umgebung von $ x_0$ . Ist $ \nabla f(x_0)=0$ und $ \mathrm{H}_f(x_0)$ positiv definit (bzw. negativ definit), so besitzt $ f$ ein lokales Minimum (bzw. lokales Maximum) an der Stelle $ x_0$ .

Ist $ \nabla f(x_0)=0$ und $ \mathrm{H}_f(x_0)$ indefinit, so nennt man $ x_0$ einen Sattelpunkt von $ f$ . Es gibt dann für alle $ \varepsilon>0$ Punkte $ x_1,\, x_2\,\in\, B_\varepsilon(x_0)$ mit $ f(x_1) < f(x_0) < f(x_2)$ .

Multiplikatorenregel von Lagrange.

Sei $ M\subseteq\mathbb{R}^n$ . Seien $ f:M\to\mathbb{R}$ und $ g: M \to \mathbb{R}^m$ . Sei $ V(g) := \{x\in M\; :\; g(x) = 0\}$ die Menge der Nullstellen von $ g$ auf $ M$ .

Wir sagen, $ f$ besitzt ein lokales Minimum (bzw. lokales Maximum, bzw. lokales Extremum) unter der Nebenbedingung $ g=0$ an der Stelle $ x_0\in M$ , falls $ x_0\in V(g)$ und falls $ f\vert _{V(g)}$ bei $ x_0$ ein lokales Minimum (bzw. lokales Maximum, bzw. lokales Extremum) besitzt.

Notwendige Bedingung. Sei $ M\subseteq\mathbb{R}^n$ offen, und seien $ f:M\to\mathbb{R}$ und $ g: M \to \mathbb{R}^m$ stetig differenzierbar. Hat $ f$ ein lokales Extremum an der Stelle $ x_0$ unter der Nebenbedingung $ g=0$ , und gilt $ \operatorname{Rang } g'(x_0)=m$ , so gibt es ein $ \lambda \in \mathbb{R}^m$ mit $ f'(x_0) = \lambda^\mathrm{t} g'(x_0)$ . Der Vektor $ \lambda$ heißt Lagrangescher Multiplikator.

Diese Bedingung leitet sich folgendermaßen her. Ein Vektor an $ x_0$ in $ \mathbb{R}^n$ steht tangential zu $ V(g)$ genau dann, wenn er im Kern von $ g'(x_0)$ liegt. Notwendige Bedingung für ein lokales Minimum ist, daß entlang dieser Tangentialrichtungen die Richtungsableitung von $ f$ verschwindet. Es sollte also ein Vektor im Kern von $ g'(x_0)$ auch im Kern von $ f'(x_0)$ liegen, d.h. der Kern der gestapelten Matrix $ \begin{pmatrix}g'(x_0) \\ f'(x_0)\end{pmatrix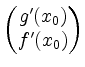}$ sollte gleich dem Kern von $ g'(x_0)$ sein. Aus Ranggründen muß also $ f'(x_0)$ im Erzeugnis des Zeilenraumes von $ g'(x_0)$ liegen.

Setze $ F(x) := f(x) - \lambda g(x)$ für $ x\in M$ .

Ein Punkt $ x_0\in V(g)\,$ , der innerer Punkt von $ M$ ist, und für den $ F'(x_0) = 0$ und $ \operatorname{Rang } g'(x_0)=m$ gilt, heißt regulärer kritischer Punkt. Ein regulärer kritischer Punkt ist also ein Kandidat für eine lokale Extremstelle unter der Nebenbedingung $ g=0$ , welcher (dank $ \operatorname{Rang } g'(x_0)=m$ , i.e. dank Regularität) mit den Lagrangeschen Methoden behandelt werden kann.

Hinreichende Bedingung. Sei $ M\subseteq\mathbb{R}^n$ offen, und seien $ f:M\to\mathbb{R}$ und $ g: M \to \mathbb{R}^m$ zweimal stetig differenzierbar, sei $ g(x_0) = 0$ , und sei $ \operatorname{Rang } g'(x_0)=m$ . Enthalte die Matrix $ \mathrm{T}_g(x_0)\in\mathbb{R}^{n\times(n-m)}$ in den Spalten ein Basis des Kerns von $ g'(x_0)$ , i.e. sei $ \operatorname{Bild } \mathrm{T}_g(x_0) = \operatorname{Kern }g'(x_0)$ . Sei wieder $ F(x) := f(x) - \lambda g(x)$ , und zwar nun mit dem Lagrange-Multiplikator $ \lambda$ an der Stelle $ x_0$ , den man aus der notwendigen Bedingung erhält, i.e. für den $ f'(x_0) = \lambda^\mathrm{t} g'(x_0)$ ist.

Ist nun die relative Hessematrix

$\displaystyle \mathrm{H}_{f;g}(x_0) \; :=\; \mathrm{T}_g(x_0)^\mathrm{t}\, \mathrm{H}_F(x_0) \mathrm{T}_g(x_0) \;\in\; \mathbb{R}^{(n-m)\times (n-m)} $

positiv definit (bzw. negativ definit, bzw. definit), so besitzt $ f$ ein lokales Minimum (bzw. lokales Maximum, bzw. lokales Extremum) unter der Nebenbedingung $ g=0$ an der Stelle $ x_0\in M$ .

Beachte, daß die relative Hessematrix $ \mathrm{H}_{f;g}(x_0)$ nicht nur von $ g$ und $ x_0$ , sondern auch von der Wahl der Basis des Kerns von $ g'(x_0)$ abhängt.

Diese Bedingung leitet sich folgendermaßen her. Lokal bei $ x_0$ können wir $ V(g)$ wie folgt beschreiben. Sei $ T := \mathrm{T}_g(x_0)$ eine Matrix, deren Spalten eine Basis des Kerns von $ g'(x_0)$ bilden. Sei $ N := \mathrm{N}_g(x_0)$ so, daß $ g'(x_0) N = \mathrm{E}_m$ .

Beachte, daß dann insbesondere $ f'(x_0) T = \lambda^\mathrm{t} g'(x_0) T = 0$ und $ f'(x_0) N = \lambda^\mathrm{t} g'(x_0) N = \lambda^\mathrm{t}$ sind.

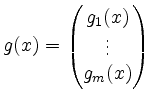Wir fragen uns, wie $ z\in\mathbb{R}^m$ von $ y\in\mathbb{R}^{n-m}$ abhängt, so daß $ g(x_0 + T y + N z) = 0$ ist. Bis auf Glieder von Ordnung $ \ge 3$ schreibt sich diese Bedingung nach Taylor mit $ g(x) = \begin{pmatrix}g_1(x)\\ \vdots\\ g_m(x)\end{pmatrix}$ als

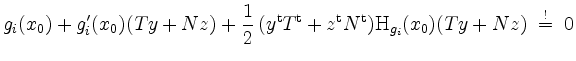
$\displaystyle g_i(x_0) + g_i'(x_0)(T y + N z) + \frac{1}{2}\, (y^\mathrm{t} T^\... ...hrm{t} N^\mathrm{t}) \mathrm{H}_{g_i}(x_0) (T y + N z) \; \stackrel{!}{=} \; 0 $

für alle $ 1\le i\le m$ . Nun ist $ g(x_0) = 0$ . Ferner ist $ g'(x_0) T = 0$ . Desweiteren kann man $ y$ als klein von erster Ordnung, und $ z$ als klein von zweiter Ordnung ansehen. Bleibt

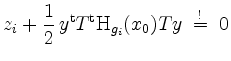
$\displaystyle z_i + \frac{1}{2}\, y^\mathrm{t} T^\mathrm{t} \mathrm{H}_{g_i}(x_0) T y \; \stackrel{!}{=} \; 0 $

für alle $ 1\le i\le m$ , also $ z_i = z_i(y) = - \frac{1}{2}\, y^\mathrm{t} T^\mathrm{t} \mathrm{H}_{g_i}(x_0) T y$ .

Setzen wir nun $ x_0 + Ty + N z(y)$ in $ f$ ein! Wir müssen nach Einsetzen das Extremalverhalten bei $ y = 0$ untersuchen. Bis auf Glieder von Ordnung $ \ge 3$ erhalten wir dabei mit Taylor

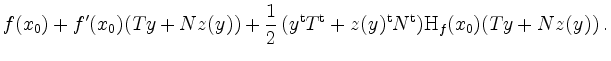
$\displaystyle f(x_0) + f'(x_0)(Ty + N z(y)) + \frac{1}{2}\, (y^\mathrm{t} T^\mathrm{t} + z(y)^\mathrm{t} N^\mathrm{t}) \mathrm{H}_f(x_0) (Ty + N z(y))\; . $

Nun ist die Konstante $ f(x_0)$ für die Frage nach der Extremalität belanglos, es ist $ f'(x_0) Ty = 0$ , es ist $ f'(x_0) N = \lambda^\mathrm{t}$ , und es ist $ y$ klein von erster, sowie dann $ z(y)$ klein von zweiter Ordnung. Bleibt

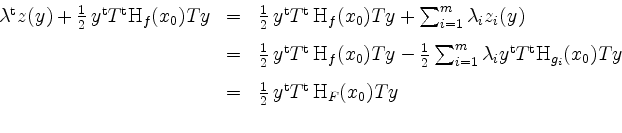
\begin{displaymath} \begin{array}{rcl} \lambda^\mathrm{t} z(y) + \frac{1}{2}\, y... ...\mathrm{t}\,\mathrm{H}_F(x_0) T y \vspace*{3mm} \\ \end{array}\end{displaymath}

zu betrachten, welches in $ y = 0$ genau dann ein lokales Maximum (resp. Minimum) hat, wenn $ T^\mathrm{t} \mathrm{H}_F(x_0) T$ negativ (resp. positiv) definit ist.

Praktische Anwendung der Multiplikatorenregel von Lagrange.

Setze $ F(x) = f(x) - \lambda^\mathrm{t} g(x)$ , mit einem zunächst unbekannten Vektor $ \lambda \in \mathbb{R}^m$ . Um die regulären kritischen Punkte zu ermitteln, löse man

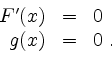
\begin{displaymath} \begin{array}{rcl} F'(x) & = & 0 \\ g(x) & = & 0 \; .\\ \end{array}\end{displaymath}

Das sind $ n + m$ Gleichungen ($ n$ von $ F'$ , $ m$ von $ g$ ) für $ n + m$ Unbekannte ($ n$ von $ x$ , $ m$ von $ \lambda$ ). Ist $ x_0\in\mathbb{R}^n$ zusammen mit einem gewissen $ \lambda \in \mathbb{R}^m$ Lösung des Systems, und gilt $ \operatorname{Rang } g'(x_0)=m$ , so ist $ x_0$ ein regulärer kritischer Punkt.

Sei nun $ x_0$ ein regulärer kritischer Punkt. Wir wollen ihn auf Extremalität hin untersuchen. Bilde mit dem bei $ x_0$ erhaltenen Lagrangemultiplikator $ \lambda \in \mathbb{R}^m$ die Funktion $ F = f - \lambda g$ .

Berechne eine Basis des Kerns von $ g'(x_0)$ , und schreibe diese Basis als Spalten in die Matrix $ \mathrm{T}_g(x_0)\in\mathbb{R}^{n\times(n-m)}$ . Untersuche die relative Hessematrix $ \mathrm{H}_{f;g}(x_0) = \mathrm{T}_g(x_0)^\mathrm{t}\, \mathrm{H}_F(x_0) \mathrm{T}_g(x_0)$ auf Definitheit. Ist sie positiv definit (resp. negativ definit), so liegt in $ x_0$ ein lokales Minimum (resp. lokales Maximum) von $ f$ unter Nebenbedingung $ g=0$ vor.

Für verschiedene zu untersuchende reguläre kritische Punkte ist es günstig, sogleich für ein beliebiges konstantes $ \lambda \in \mathbb{R}^m$ und beliebiges $ x\in M$ die Hessematrix $ \mathrm{H}_F(x)$ zu bilden, um dann bei Bedarf Werte einzusetzen.

Vergleiche Barner, Flohr, Analysis II, Kap. 14.7, Aufgabe 15; Jank, Jongen, Höhere Mathematik II für Maschinenbauer, Aachener Beitr. Math. 4, Satz 8.4.12; oder Maurin, K., Analysis. Part I., Th. VIII.4.5, wo dieses hinreichende Lagrangekriterium Wiktor Szczyrba zugeschrieben wird.

(Autoren: Künzer/Martin/Tentler/Wahrheit)
[Beispiele] [Verweise]
  automatisch erstellt am 22.  8. 2006