Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
Mathematik-Online-Lexikon:

Ein zweidimensionales Riemann-Integral

A B C D E F G H I J K L M N O P Q R S T U V W X Y Z Übersicht

Berechne 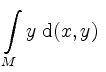$ \displaystyle\int\limits_M y \;\mathrm{d}(x,y)\;$ mit $ M\;=\;\{(x,y)^\mathrm{t}\in\mathbb{R}^2\ \vert\ x^2+y^2\leq 4,\; y\geq 1\}$ .

Lösung.

Es ist $ M$ beschränkt, und der Rand von $ M$ ist eine Lebesguesche Nullmenge, also ist $ M$ meßbar. Zudem ist $ f$ eine stetige Funktion auf $ M$ , also auch integrierbar über $ M$ . Wir bilden den $ y$ -Schnitt

\begin{displaymath} M^y \; =\; \{x\in\mathbb{R}\ \vert\ x^2+y^2\leq 4,\ y\geq 1\... ...falls $y\in [1,2]$}\\ \emptyset, & \mathrm{sonst} \end{cases}\end{displaymath}

sowie

$\displaystyle M''\;=\;\{y\in\mathbb{R}\ \vert\ M^y\neq\emptyset\}=[1,2]\;. $

Diese Mengen sind meßbar, also folgt

\begin{displaymath} \begin{array}{rcl} \displaystyle\int_M y\; \mathrm{d}(x,y) &... ...c{2}{3} (4-y^2)^{3/2}\right]_1^2 \;=\; 2\sqrt{3}\;. \end{array}\end{displaymath}

(Autoren: Künzer/Martin/Tentler/Wahrheit)
[Verweise]
  automatisch erstellt am 11.  8. 2006