Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
Mathematik-Online-Lexikon:

Fourierentwicklung zur Berechnung des Wertes einer Reihe

A B C D E F G H I J K L M N O P Q R S T U V W X Y Z Übersicht

1.
Berechne die komplexe Fourierentwicklung von $ f(x) = x$ auf $ [0,2\pi)$ , $ 2\pi$ -periodisch fortgesetzt.
2.
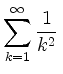Verwende die Parsevalsche Normgleichung zur Berechnung von $ \displaystyle\sum_{k = 1}^\infty \frac{1}{k^2}\,$ .

Lösung.

1.
Wir erhalten für $ k\ne 0$

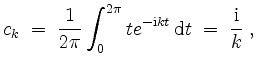
$\displaystyle c_k \;=\; \frac{1}{2\pi} \int_0^{2\pi} t e^{-\mathrm{i} kt}\,\mathrm{d}t \;=\; \frac{\mathrm{i}}{k}\; , $

sowie

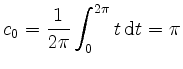
$\displaystyle c_0 = \frac{1}{2\pi} \int_0^{2\pi} t\,\mathrm{d}t = \pi $

und somit

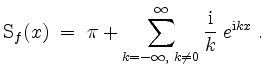
$\displaystyle \mathrm{S}_f(x) \;=\; \pi + \sum_{k = -\infty,\; k\ne 0}^{\infty} \frac{\mathrm{i}}{k}\; e^{\mathrm{i} kx} \; . $

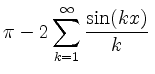Skizze des Graphen der ersten $ 4$ und des Graphen der ersten $ 20$ Summanden der zugehörigen reellen Fourierreihe $ \pi - 2\displaystyle\sum_{k = 1}^\infty \frac{\sin(kx)}{k}\,$ .

\includegraphics[width = 12cm, height = 8cm]{saege.eps}

2.
Die Parsevalsche Normgleichung gibt

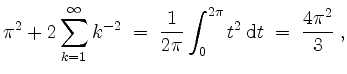
$\displaystyle \pi^2 + 2\sum_{k = 1}^{\infty} k^{-2} \;=\; \frac{1}{2\pi}\int_0^{2\pi} t^2\,\mathrm{d}t \;=\; \frac{4\pi^2}{3}\; , $

also

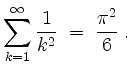
$\displaystyle \sum_{k = 1}^{\infty} \frac{1}{k^2} \;=\; \frac{\pi^2}{6}\; . $

Zum Vergleich, es sind

\begin{displaymath} \begin{array}{rcl} \displaystyle\sum_{k = 1}^{10} k^{-2} & \... ...& \approx & 1.644934066848226436472415166646\,. \\ \end{array}\end{displaymath}

Die auffällige Übereinstimmung weiterer Dezimalen erklärt sich (zum Teil) mittels der guten Näherung des Restes durch

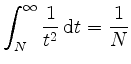
$\displaystyle \int_N^\infty \frac{1}{t^2}\,\mathrm{d}t = \frac{1}{N} $

für $ N > 0\,$ .
(Autoren: Künzer/Martin/Tentler/Wahrheit)
[Verweise]
  automatisch erstellt am 11.  8. 2006