
Mathematik-Online-Lexikon:

|
[Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen] |
|
Mathematik-Online-Lexikon: | |
Stromfluss in einem Schwingkreis |
| A B C D E F G H I J K L M N O P Q R S T U V W X Y Z | Übersicht |
Bestimme die allgemeine Lösung von
Diese Gleichung beschreibt den Stromfluß
Lösung.
Wir wollen den in der Wiederholung mit III bezeichneten Lösungsweg verwenden.
Wir setzen hierzu
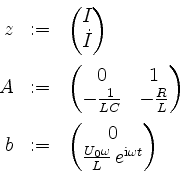
und lösen
Wir wollen ![]() berechnen. Da die Matrix
berechnen. Da die Matrix
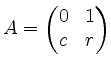 Parameter enthält, gehen wir näher auf diese Berechnung ein. Ihre Eigenwerte sind
Parameter enthält, gehen wir näher auf diese Berechnung ein. Ihre Eigenwerte sind
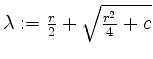 und
und
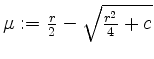 , und nach Voraussetzung an
, und nach Voraussetzung an ![]() verschieden und beide reell.
verschieden und beide reell.
Die Jordanform ergibt sich zu
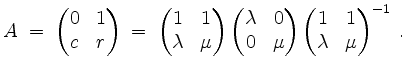
Somit ist
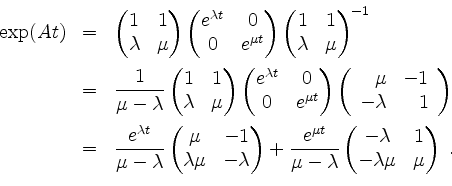
Für die Variation der Konstanten beachten wir zunächst, daß wir nach Ersetzen von ![]() durch
durch ![]()
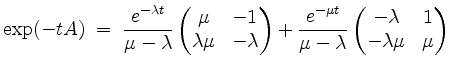
erhalten. Nun wird, für beliebig wählbare Konstanten
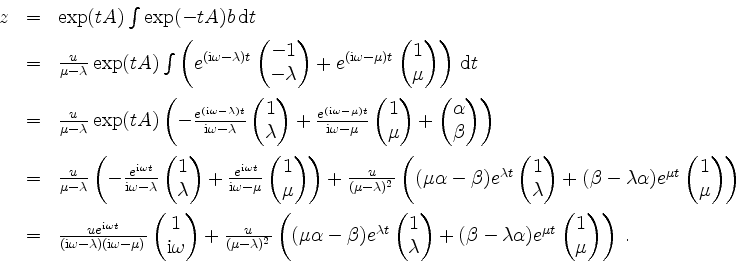
Reskalieren der Konstanten
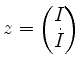 liefert die allgemeine Lösung
liefert die allgemeine Lösung
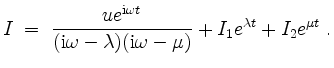
Da wir anstelle von
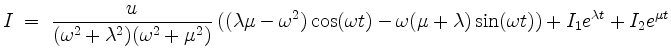
liefert. Teilweises Rückeinsetzen der ursprünglichen Größen
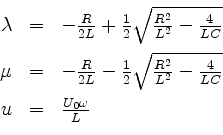
bringt die allgemeine Lösung auf die Form
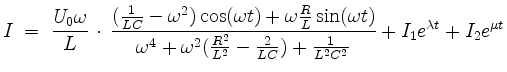
für
Skizze für ![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
,
![]() (von oben nach unten),
(von oben nach unten),
![]() und
und ![]() .
.
![\includegraphics[width = 8cm]{RCL.eps}](/inhalt/beispiel/beispiel1175/img45.png)
Interpretation. Nach Abklingen des homogenen Bestandteils
![]() verbleibt für große
verbleibt für große ![]() eine Schwingung mit Frequenz
eine Schwingung mit Frequenz ![]() gleich der Erregerfrequenz.
Die Phasenverschiebung im Vergleich zur Erregerspannung, sowie die Amplitude können der oben hergeleiteten Formel entnommen werden.
gleich der Erregerfrequenz.
Die Phasenverschiebung im Vergleich zur Erregerspannung, sowie die Amplitude können der oben hergeleiteten Formel entnommen werden.
| automatisch erstellt am 11. 8. 2006 |