Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen] Englische Flagge
Mathematik-Online-Lexikon:

Ableitung im Raum der Polynome

A B C D E F G H I J K L M N O P Q R S T U V W X Y Z Übersicht

Zur Illustration der Dimensionsformel wird die $ k$-te Ableitung auf dem Raum der Polynome von Grad $ \le n$ betrachtet.

Sei zunächst $ k=1$ und $ n=2$. Für den Raum der Polynome vom Grad $ \le 2$ bildet $ \{1,x,x^2\}$ eine Basis, der Raum hat also Dimension 3. Für $ p(x)=a_0+a_1x+a_2x^2$ ist $ p'(x)=a_1+2a_2x$ ein Polynom vom Grad $ \le 1$. Der Bildraum hat also Dimension 2. Beim Ableiten verschwinden die Konstanten. Diese bilden einen eindimensionalen Unterraum. Der Kern der Abbildung hat also Dimension 1 und somit ist die Dimensionsformel mit $ 3=1+2$ erfüllt.

Im allgemeinen Fall hat das Polynom die Form

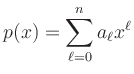
$\displaystyle p(x)=\sum_{\ell =0}^n a_\ell x^\ell $

und die $ k$-te Ableitung

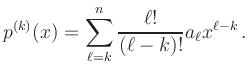
$\displaystyle p^{(k)}(x)=\sum_{\ell =k}^n \frac{\ell !}{(\ell -k)!}a_\ell x^{\ell -k}\,. $

Das Bild ist ein Polynom vom Grad $ \le n-k$ und Polynome vom Grad $ <k$ werden annulliert. Die Dimensionsformel hat also die Form

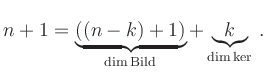
$\displaystyle n+1=\underbrace{((n-k)+1)}_{\dim \operatorname{Bild}} + \underbrace{k}_{\dim \operatorname{ker}}\,. $

siehe auch:

  automatisch erstellt am 25.  6. 2018