Mathematik-Online-Aufgabensammlung: Lösung zu: Aufgabe 882: Länge und Schwerpunkt einer Kettenlinie

	[Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
	Mathematik-Online-Aufgabensammlung: Lösung zu
	Aufgabe 882: Länge und Schwerpunkt einer Kettenlinie

A B C D E F G H I J K L M N O P Q R S T U V W X Y Z

Ist $\mbox{$f:[a,b]\longrightarrow \mathbb{R}$}$ eine differenzierbare Funktion, so berechnet sich die Länge seines Graphen zu

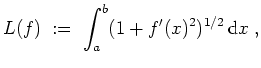
$\mbox{$\displaystyle L(f) \; :=\; \int_a^b (1+f'(x)^2)^{1/2}\,{\mbox{d}}x\; , $}$

und die Höhe seines Schwerpunktes zu

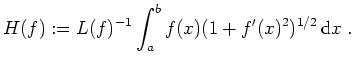
$\mbox{$\displaystyle H(f) := L(f)^{-1}\int_a^b f(x)(1+f'(x)^2)^{1/2}\,{\mbox{d}}x\; . $}$

(1): Sei $\mbox{$f:[-1,+1]\longrightarrow \mathbb{R}$}$ mit $\mbox{$f(x) := \cosh x - \cosh 1$}$ . Berechne $\mbox{$L(f)$}$ .
(2): Berechne $\mbox{$H(f)$}$ . Vergleiche mit der Höhe des Schwerpunktes eines "dreieckigen" Polygonzuges gleicher Länge durch Punkte $\mbox{$(-1,0)$}$ , $\mbox{$(0,-a)$}$ , $\mbox{$(+1,0)$}$ für ein $\mbox{$a\in\mathbb{R}_{\geq 0}$}$ .
(3): Berechne den Umfang eines Kreises von Radius $\mbox{$1$}$ unter Verwendung der Funktion $\mbox{$g(x) = \sqrt{1 - x^2}$}$ .

(1)

Die Länge des Graphen von $\mbox{$f$}$ ist

$\mbox{$\displaystyle \begin{array}{rcl} L(f) & = & \int_{-1}^{+1} (1 + f'(x)... ... = & [\sinh x]_{-1}^{+1} \vspace*{2mm}\\ & = & e - 1/e\; . \\ \end{array}$}$

(2)

Der Schwerpunkt des Graphen von $\mbox{$f$}$ hat die Höhe

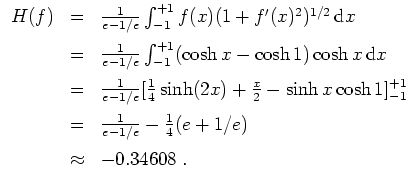
$\mbox{$\displaystyle \begin{array}{rcl} H(f) & = & \frac{1}{e - 1/e}\int_{-1}... ...\frac{1}{4}(e + 1/e) \vspace*{2mm}\\ & \approx & -0.34608 \; . \end{array}$}$

Für den verlangten Polygonzug ist $\mbox{$2(1 + a^2)^{1/2} = L(f)$}$ , und somit $\mbox{$a = ((L(f)/2)^2 - 1)^{1/2} = \frac{1}{2}(e^2 + e^{-2} - 6)^{1/2}$}$ . Er hat den Schwerpunkt in Höhe

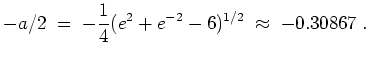
$\mbox{$\displaystyle -a/2 \; =\; -\frac{1}{4}(e^2 + e^{-2} - 6)^{1/2} \; \approx\; -0.30867 \; . $}$

Skizze $\mbox{$f$}$ und "Dreiecklinie".

$\includegraphics[width=10cm]{s2_cosh.eps}$

(3)

Für den halben Kreisumfang erhalten wir mit $\mbox{$g:[-1,+1]\longrightarrow \mathbb{R}$}$ , $\mbox{$g(x) = (1 - x^2)^{1/2}$}$ und $\mbox{$g'(x) = -x\cdot (1 - x^2)^{-1/2}$}$ den Wert

$\mbox{$\displaystyle L(g) \; =\; \int_{-1}^{+1} \left( 1 + x^2\cdot (1 - x^2)... ...{+1} (1-x^2)^{-1/2}\,{\mbox{d}}x \; =\; [\arcsin x]_{-1}^{+1} \; =\; \pi\; . $}$

Der Umfang eines Kreises mit Radius $\mbox{$1$}$ beträgt somit $\mbox{$2\pi$}$ .

(Autoren: Künzer/Martin/Nebe)

[Zurück zur Aufgabe]

automatisch erstellt am 7. 6. 2005