Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
Mathematik-Online-Aufgabensammlung: Lösung zu

Aufgabe 1131: Produkte von Dreiecksmatrizen

A B C D E F G H I J K L M N O P Q R S T U V W X Y Z

Wir betrachten zwei beliebige $ 3\times3$-Matrizen $ A,B$. Verifizieren Sie:

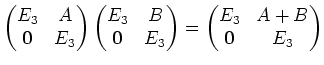
$\displaystyle \left(\begin{matrix} E_3 & A \\ \mathbf{0} & E_3 \end{matrix}\ri... ...ght) = \left(\begin{matrix} E_3 & A+B \\ \mathbf{0} & E_3 \end{matrix}\right) $

(Zur Erinnerung: $ E_3$ ist die $ 3\times3$-Einheitsmatrix, $ \mathbf{0}$ ist in diesem Fall die $ 3\times3$-Nullmatrix).

Zur besseren Verständigung geben wir unseren Matrizen Namen:

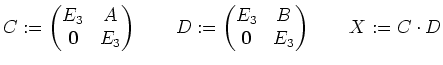$\displaystyle C:=\left(\begin{matrix}E_3 & A \\ \mathbf{0} & E_3 \end{matrix}\r... ...begin{matrix}E_3 & B \\ \mathbf{0} & E_3 \end{matrix}\right) \qquad X:=C\cdot D$    

Wir erinnern uns daran, dass $ x_{k\ell}=\sum_{j=1}^6 c_{kj}d_{j\ell}$. Nun müssen wir 4 Fälle unterscheiden:
\begin{displaymath}\begin{array}[t]{c\vert c}*&\cdot\\ \hline\cdot&\cdot\end{array}\end{displaymath}
Einträge im linken oberen Viertel (also $ 1\leq k\leq3$, $ 1\leq\ell\leq 3$):
Wegen $ \ell\le3$ gilt jedenfalls $ d_{j\ell}=0$ für $ j\ge4$, und damit $ x_{k\ell}=\sum_{j=1}^3 c_{kj}d_{j\ell}$.
Für $ j\le3$ haben wir $ c_{kj}=1$ für $ j=k$ und $ c_{kj}=0$ für $ j\neq k$.
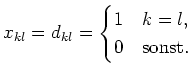Daher ist      $ x_{kl}=d_{kl}=\begin{cases}1 & k=l, \\ 0 & \text{sonst.}\end{cases}$          Also wissen wir $ X=\left(\begin{array}[c]{c\vert c}E_3&?\\ \hline?&?\end{array}\right)$.
\begin{displaymath}\begin{array}[t]{c\vert c}\cdot&\cdot\\ \hline\cdot&*\end{array}\end{displaymath}
Einträge im rechten unteren Viertel (also $ 4\leq k\leq6$, $ 4\leq\ell\leq 6$):
Wegen $ \ell\ge4$ gilt jedenfalls $ c_{kj}=0$ für $ j\le3$, und damit $ x_{k\ell}=\sum_{j=4}^6 c_{kj}d_{j\ell}$.
Für $ j\ge4$ haben wir $ d_{j\ell}=1$ für $ j=\ell$ und $ d_{j\ell}=0$ für $ j\neq \ell$.
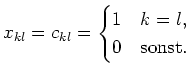Daher ist      $ x_{kl}=c_{kl}=\begin{cases}1 & k=l, \\ 0 & \text{sonst.}\end{cases}$          Also wissen wir $ X=\left(\begin{array}[c]{c\vert c}E_3&?\\ \hline?&E_3\end{array}\right)$.
\begin{displaymath}\begin{array}[t]{c\vert c}\cdot&\cdot\\ \hline*&\cdot\end{array}\end{displaymath}
Einträge im linken unteren Viertel (also $ 4\leq k\leq6$, $ 1\leq l\leq 3$): Hier gilt
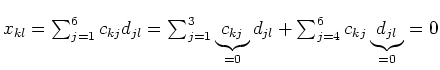$ x_{kl}=\sum_{j=1}^6 c_{kj}d_{jl}= \sum_{j=1}^3 \underbrace{c_{kj}}_{=0}d_{jl}+\sum_{j=4}^6 c_{kj}\underbrace{d_{jl}}_{=0}=0$, also $ X=\left(\begin{array}[c]{c\vert c}E_3&?\\ \hline0&E_3\end{array}\right)$.
\begin{displaymath}\begin{array}[t]{c\vert c}\cdot&*\\ \hline\cdot&\cdot\end{array}\end{displaymath}
Einträge im rechten oberen Viertel (also $ 1\leq k\leq3$, $ 4\leq l\leq 6$): Hier gilt
$ x_{kl}=\sum_{j=1}^6 c_{kj}d_{jl}=\sum_{j=1}^3 c_{kj}d_{jl}+\sum_{j=4}^6 c_{kj}d_{jl}=d_{kl}+c_{kl}$, also $ X=\left(\begin{array}[c]{c\vert c}E_3&A+B\\ \hline0&E_3\end{array}\right)$.
Damit ist alles gezeigt.


(Ackermann/Poppitz)
[Zurück zur Aufgabe]
  automatisch erstellt am 19. 12. 2005