Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
Mathematik-Online-Aufgabensammlung: Lösung zu

Aufgabe 1214: Diagonalisieren einer Matrix sowie Bestimmen einer Diagonalmatrix und einer Transformationsmatrix

A B C D E F G H I J K L M N O P Q R S T U V W X Y Z
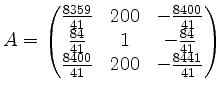Diagonalisieren Sie die Matrix $ A = \left(\begin{matrix} \frac{8359}{41} & 200 &-\frac{8400}{41} \\ \frac{84}... ...-\frac{84}{41} \\ \frac{8400}{41} & 200 &-\frac{8441}{41} \end{matrix}\right)$. Bestimmen Sie eine Diagonalmatrix $ D$, zu der $ A$ konjugiert ist, und die Transformationsmatrix $ T$, für die $ D=T^{-1}A\,T$ gilt.

Die Matrix $ A$ soll diagonalisiert werden. Dazu müssen die Eigenwerte und Eigenvektoren von $ A$ bestimmt werden. Die Eigenwerte sind $ \lambda_1=1$ und $ \lambda_2=-1$.

Wir bestimmen nun, wie im Hinweis empfohlen, den Eigenraum zum Eigenwert $ \lambda_2$ und erhalten

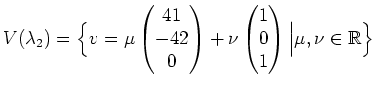
$\displaystyle V(\lambda_2)=\Big{\{}v=\mu \begin{pmatrix}41\\ -42\\ 0 \end{pmatr... ...u\begin{pmatrix}1\\ 0\\ 1 \end{pmatrix} \Big\vert\mu,\nu\in\mathbb{R} \Big{\}} $

(dies lässt sich auch ohne Taschenrechner bestimmen!); wir sehen damit auch, dass $ \lambda_2$ ein doppelter Eigenwert sein muss, da der zugehörige Eigenraum 2-dimensional ist. Wir haben also den 2-dimensionalen Eigenraum $ V(\lambda_2)$ und den 1-dimensionalen Eigenraum $ V(\lambda_1)=\operatorname{Span}(v_1)$.

Daraus können wir also eine Basis aus Eigenvektoren wählen, zum Beispiel:

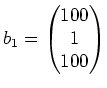
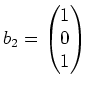
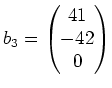$ b_1=\begin{pmatrix}100\\ 1\\ 100 \end{pmatrix}$ $ b_2=\begin{pmatrix}1\\ 0\\ 1 \end{pmatrix} $ $ b_3=\begin{pmatrix}41\\ -42\\ 0 \end{pmatrix} $.

Dies liefert uns die Transformationsmatrix

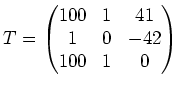
$\displaystyle T=\left(\begin{matrix} 100 & 1 & 41 \\ 1 & 0 &-42 \\ 100 & 1 & 0 \end{matrix}\right) $

und die Diagonalmatrix (die Eigenwerte stehen in der von $ T$ vorgegebenen Reihenfolge auf der Diagonalen):

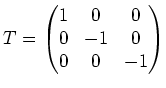
$\displaystyle T=\left(\begin{matrix} 1 & 0 & 0 \\ 0 &-1 & 0 \\ 0 & 0 & -1 \end{matrix}\right) $

(Ackermann/Poppitz)
[Zurück zur Aufgabe]
  automatisch erstellt am 6.  2. 2006