
Mathematik-Online-Aufgabensammlung: Lösung zu

|
[Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen] |
|
Mathematik-Online-Aufgabensammlung: Lösung zu | |
Aufgabe 1332: Extrema mit Nebenbedingungen |
| A B C D E F G H I J K L M N O P Q R S T U V W X Y Z |
unter den Nebenbedingungen
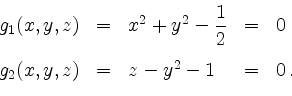
Setze
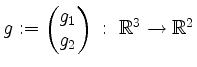 . Die Funktionen
. Die Funktionen ![]() ,
, ![]() und
und ![]() sind beliebig oft stetig differenzierbar.
sind beliebig oft stetig differenzierbar.
Sei
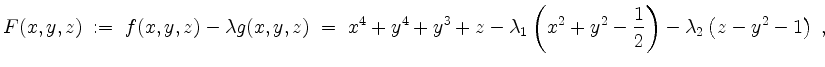
wobei
Die Ableitung von ![]() berechnet sich zu
berechnet sich zu
Aus der notwendigen Bedingung für lokale Extrema
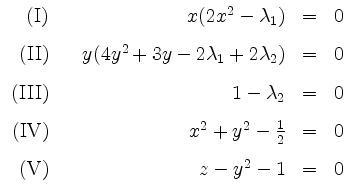
Gleichung (III) gibt
Für den Fall, daß ![]() und
und ![]() , vereinfachen sich die Gleichungen (I) und (II) zu
, vereinfachen sich die Gleichungen (I) und (II) zu
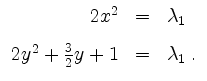
Gleichsetzen der linken Seiten gibt
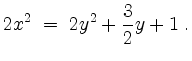
Mit Gleichung (IV) erhalten wir
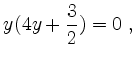
d.h.
Falls ![]() , so ist wegen (IV) zunächst
, so ist wegen (IV) zunächst
![]() , und wegen (V) ist
, und wegen (V) ist
![]() . Gleichung (II) kann nun noch mit
. Gleichung (II) kann nun noch mit
![]() erfüllt werden. Wir erhalten die kritischen Punkte
erfüllt werden. Wir erhalten die kritischen Punkte
![]() ,
mit
,
mit
![]() , und
, und
![]() , mit
, mit
![]() .
.
Falls ![]() , so ist wegen (IV)
, so ist wegen (IV)
![]() , und wegen (V) ist
, und wegen (V) ist ![]() . Gleichung (I) kann nun noch mit
. Gleichung (I) kann nun noch mit
![]() erfüllt werden. Wir erhalten die kritischen Punkte
erfüllt werden. Wir erhalten die kritischen Punkte
![]() und
und
![]() ,
bei welchen
,
bei welchen
![]() ist.
ist.
Es ist
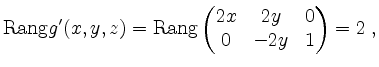
sofern
Untersuchen wir nun unsere kritischen Punkte auf lokale Extrema vermittels der relativen Hessematrix. Halten wir zunächst fest, daß
sich für ![]() und
und ![]() beliebig
beliebig
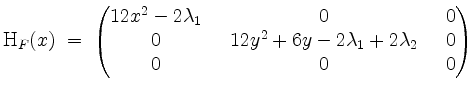
ergibt.
Im folgenden fassen wir Vorzeichen zusammen, falls sich dies anbietet.
Im kritischen Punkt
![]() ist
ist
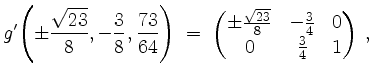
und wir können
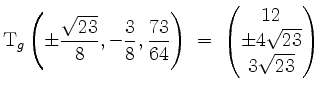
setzen. Wegen
Da die relative Hessematrix infolgedessen positiv definit ist, liegt für beide Wahlen des Vorzeichens ein lokales Minimum unter Nebenbedingung
![]() vor.
vor.
Im kritischen Punkt
![]() ist
ist
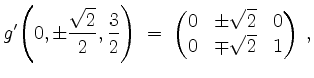
und wir können
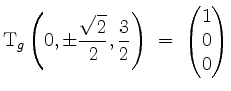
setzen. Wegen
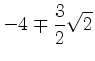
Da die relative Hessematrix infolgedessen bei beiden Wahlen des Vorzeichens negativ definit ist, liegt für beide Wahlen des Vorzeichens ein lokales Maximum unter Nebenbedingung
Im kritischen Punkt
![]() ist
ist
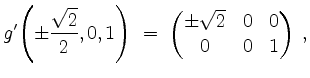
und wir können
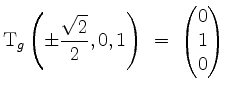
setzen. Wegen
Die Menge ![]() ist wegen der Gestalt von
ist wegen der Gestalt von ![]() beschränkt, wegen der Stetigkeit von
beschränkt, wegen der Stetigkeit von ![]() abgeschlossen, und also insgesamt kompakt.
Da ferner
abgeschlossen, und also insgesamt kompakt.
Da ferner ![]() stetig ist, nimmt
stetig ist, nimmt ![]() ein globales Maximum und ein globales Minimum auf
ein globales Maximum und ein globales Minimum auf ![]() an. Unbeschadet unserer nur hinreichenden Bedingung
mit der relativen Hessematrix müssen beide unter den sechs regulären kritischen Punkten auftauchen, da
an. Unbeschadet unserer nur hinreichenden Bedingung
mit der relativen Hessematrix müssen beide unter den sechs regulären kritischen Punkten auftauchen, da ![]() auf ganz
auf ganz ![]() den Rang
den Rang ![]() hat.
hat.
Durch Vergleichen der Funktionswerte bei den kritischen Punkten
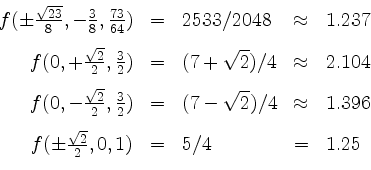
erkennen wir unschwer das globale Maximum und das globale Minimum.
Da die globale Minimalstelle auch als lokale Minimalstelle, und die globale Maximalstelle auch als lokale Maximalstelle erkannt wurde, jeweils
unter Nebenbedingung ![]() , ist auch kein Widerspruch eingetreten.
, ist auch kein Widerspruch eingetreten.
Abschließend bemerken wir, daß wir ohne relative Hessematrix, nur unter Betrachtung der Funktionswerte bei den kritischen Punkten,
den Punkt
![]() nicht als lokale Maximalstelle unter Nebenbedingung
nicht als lokale Maximalstelle unter Nebenbedingung ![]() hätten erkennen können.
Diese Argumentationsnot verschärft sich noch in Fällen, in denen
hätten erkennen können.
Diese Argumentationsnot verschärft sich noch in Fällen, in denen ![]() nicht kompakt ist, man also nicht allein durch Betrachten
der Werte an den kritischen Punkten die globalen Extrema erkennen kann.
nicht kompakt ist, man also nicht allein durch Betrachten
der Werte an den kritischen Punkten die globalen Extrema erkennen kann.
| automatisch erstellt am 11. 8. 2006 |