Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
Mathematik-Online-Aufgabensammlung: Lösung zu

Aufgabe 1399: ausführliche Kurvendiskussion

A B C D E F G H I J K L M N O P Q R S T U V W X Y Z
Führen Sie eine Kurvendiskussion der Funktionen $ f$, $ g$, und $ h$ durch, welche durch die Zuordnungsvorschriften

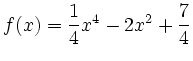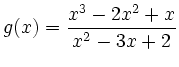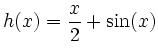
$ f(x)= \dfrac{1}{4}x^4-2x^2+\dfrac{7}{4}$, $ g(x)= \dfrac{x^3-2x^2+x}{x^2-3x+2}$, $ h(x)= \dfrac{x}{2}+\sin(x)$

gegeben sind. Bearbeiten Sie dazu insbesondere die folgenden Schritte.

a)
Bestimmen Sie den Definitionsbereich.
b)
Testen Sie auf Symmetrien.
c)
Bestimmen Sie die Bereiche, in denen Stetigkeit vorliegt, und untersuchen Sie die Funktionen auf stetig hebbare Definitionslücken.
d)
Berechnen Sie Nullstellen der Funktionen.
e)
Prüfen Sie die Funktionen auf Differenzierbarkeit.
f)
Berechenen Sie Extrema und Wendepunkte.
g)
Ermitteln Sie das Verhalten an den Rändern des Definitionsbereiches und bestimmen Sie damit senkrechte oder waagrechte Asymptoten.
h)
Skizzieren Sie den Graphen der Funktionen.
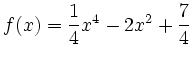
$ f(x)= \dfrac{1}{4}x^4-2x^2+\dfrac{7}{4}$

Die Funktion $ f$ ist auf ganz $ \mathbb{R}$ definiert.

Wegen $ f(-x)=\frac{1}{4}(-x)^4-2(-x)^2+\frac{7}{4} =\frac{1}{4}x^4-2x^2+\frac{7}{4}=f(x)$ ist $ f$ eine gerade Funktion und somit achsensymmetrisch.

Die Funktion ist als Polynom stetig auf ganz $ \mathbb{R}$.

Mit einer quadratischen Ergänzung

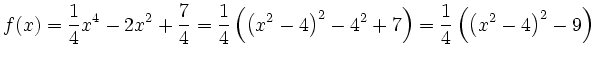
$\displaystyle f(x)= \dfrac{1}{4}x^4-2x^2+\dfrac{7}{4} %= \dfrac{1}{4}\left(x^4... ...(x^2-4\right)^2-4^2+7\right) = \dfrac{1}{4}\left(\left(x^2-4\right)^2-9\right) $

ergeben sich die Nullstellen

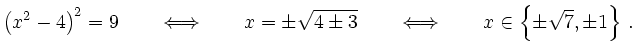
$\displaystyle \left(x^2-4\right)^2=9 \qquad \Longleftrightarrow \qquad x= \pm... ...\qquad \Longleftrightarrow \qquad x \in \left\{\pm\sqrt{7},\pm 1 \right\} \,. $

Als Polynom ist $ f$ unendlich oft differenzierbar, und die ersten drei Ableitungen lauten

$\displaystyle f'(x) = x^3-4x\,, \qquad f''(x) = 3x^2-4\,, \qquad f'''(x) = 6x \,. $

Nullstellen der ersten Ableitung sind demnach

$\displaystyle x^3-4x = x(x^2-4) =0 \qquad \Longleftrightarrow \qquad x=0$    und $\displaystyle x=\pm 2 \,.$

Die zweite Ableitung nimmt an diesen Stellen die Werte

$\displaystyle f''(-2)=8,\qquad f''(0)=-4,\qquad f''(2)=8 $

an, also befindet sich bei $ x=\pm 2$ je ein lokales Minimum $ (\pm 2,\ -9/4)$ und an $ x=0$ ein lokales Maximum $ (0,\ 7/4)$.

Nullstellen der zweiten Ableitung sind

$\displaystyle 3x^2-4 = 0 \qquad \Longleftrightarrow \qquad x=\pm \dfrac{2}{\sqrt{3}} \,.$

Die dritte Ableitung nimmt an diesen Stellen die Werte

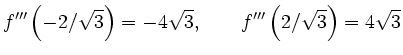
$\displaystyle f'''\left(-2/\sqrt{3}\right)=-4\sqrt{3},\qquad f'''\left(2/\sqrt{3}\right)=4\sqrt{3} $

an. Die Funktion nimmt an diesen Stellen die Werte

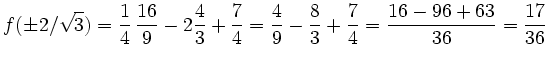
$\displaystyle f(\pm2/\sqrt{3}) =\dfrac{1}{4}\,\dfrac{16}{9}-2\dfrac{4}{3}+\dfra... ...} =\dfrac{4}{9}-\dfrac{8}{3}+\dfrac{7}{4} =\dfrac{16-96+63}{36} =\dfrac{17}{36}$

an, also befinden sich Wendepunkte in $ \left(-2/\sqrt{3},\ 17/36\right)$ und $ \left(2/\sqrt{3},\ 17/36\right)$.

Des weiteren gilt

$\displaystyle \lim_{x\to-\infty}f(x)=\lim_{x\to\infty}f(x)=+\infty\,.$

\includegraphics[width=0.5\linewidth]{h16_L_1.eps}

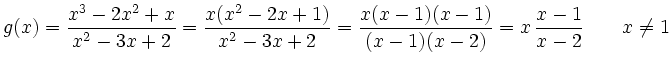
$ g(x)= \dfrac{x^3-2x^2+x}{x^2-3x+2}=\dfrac{x(x^2-2x+1)}{x^2-3x+2} =\dfrac{x(x-1)(x-1)}{(x-1)(x-2)}=x\,\dfrac{x-1}{x-2} \qquad x\neq 1$

Der Definitionsbereich von $ g$ ist $ D=\mathbb{R}\setminus\{1,2\}$.

Die Nullstelle $ x=0$ lässt sich aus der gekürzten Fassung einfach ablesen, die Stelle $ x=1$ liegt nicht im Definitionsbereich.

Als Quotient von Polynomen ist $ g$ in $ D$ differenzierbar und besitzt die Ableitungen

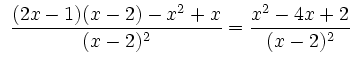$\displaystyle g'(x) =$ $\displaystyle \ \dfrac{(2x-1)(x-2)-x^2+x}{(x-2)^2}=\dfrac{x^2-4x+2}{(x-2)^2}$    
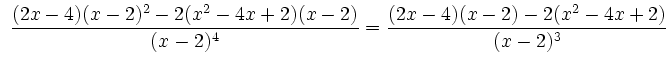$\displaystyle g''(x) =$ $\displaystyle \ \dfrac{(2x-4)(x-2)^2-2(x^2-4x+2)(x-2)}{(x-2)^4} =\dfrac{(2x-4)(x-2)-2(x^2-4x+2)}{(x-2)^3}$    
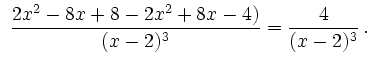$\displaystyle =$ $\displaystyle \ \dfrac{2x^2-8x+8-2x^2+8x-4)}{(x-2)^3} =\dfrac{4}{(x-2)^3} \,.$    

Die Extremstellen befinden sich also bei

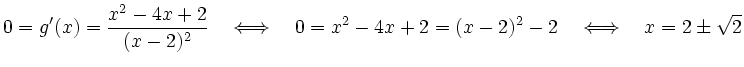
$\displaystyle 0 = g'(x) = \dfrac{x^2-4x+2}{(x-2)^2} \quad \Longleftrightarrow \... ... (x-2)^2-4+2 = (x-2)^2-2 \quad \Longleftrightarrow \quad x = 2 \pm \sqrt{2} $

mit

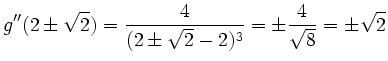
$\displaystyle g''(2\pm\sqrt{2})=\dfrac{4}{(2\pm\sqrt{2}-2)^3} =\pm\dfrac{4}{\sqrt{8}}=\pm\sqrt{2} $

und

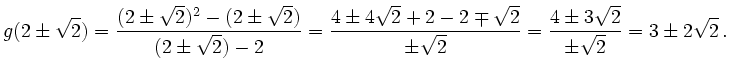
$\displaystyle g(2\pm\sqrt{2}) =\dfrac{(2\pm\sqrt{2})^2-(2\pm\sqrt{2})}{(2\pm\sq... ...qrt{2}}{\pm\sqrt{2}} =\dfrac{4 \pm 3\sqrt{2}}{\pm\sqrt{2}} =3\pm 2\sqrt{2} \,. $

Die Funktion $ g$ besitzt also das lokale Maximum $ (2-\sqrt{2},~3+2\sqrt{2})$ und das lokale Minimum $ (2+\sqrt{2},~3-2\sqrt{2})$.

Da $ g''(x)\neq 0$ ist, hat $ g$ keine Wendepunkte.

Als Grenzwerte der Funktion ergeben sich

\begin{displaymath}\begin{array}{lcc@{\hspace{1cm}}lcc} \lim\limits_{x\to-\infty... ...y\\ [1ex] \lim\limits_{x\to +\infty}g(x)&=& +\infty \end{array}\end{displaymath}

Es gibt also eine senkrechte Asymptote an $ x=2$. Außerdem ist $ g$ an $ x=1$ durch $ g(1)=0$ stetig ergänzbar.

\includegraphics[width=0.4\linewidth]{h16_L_2.eps}

$ h(x)=\dfrac{x}{2}+\sin(x)$

Der Definitionsbereich ist $ D=\mathbb{R}$.

Wegen $ h(-x)=(-x)/2+\sin(-x)=-\left(x/2+\sin(x)\right)=-h(x)$ liegt eine Symmetrie zum Ursprung vor.

$ h$ ist als Summe stetiger Funktionen stetig auf ganz $ \mathbb{R}$.

Zur Berechnung der Nullstellen lässt sich zunächst feststellen, dass $ h(0)=0/2+\sin(0)=0$ gilt, der Graph von $ h$ geht also durch den Ursprung. Aus den Eigenschaften der Sinusfunktion erhält man die Abschätzungen

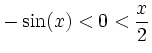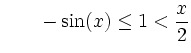$\displaystyle -\sin(x) < 0 < \dfrac{x}{2}$   für $\displaystyle x\in(0,\pi]$   und$\displaystyle \qquad -\sin(x) \le 1 < \dfrac{x}{2}$   für $\displaystyle x\in[\pi,\infty) \,. $

Insgesamt ist also $ h(x)>0$ für $ x>0$ und wegen der Symmetrie ist $ h(x)\neq 0$ genau dann, wenn $ x\neq 0$. Demnach ist $ x=0$ die einzige Nullstelle.

Die beiden Funktionen, aus denen $ h$ zusammengesetzt ist, sind beliebig oft differenzierbar, also gilt dies auch für $ h$.

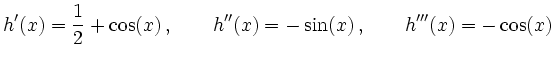
$\displaystyle h'(x) = \dfrac{1}{2}+\cos(x)\,,\qquad h''(x) = -\sin(x)\,,\qquad h'''(x) = -\cos(x) $

Extrema finden sich also bei

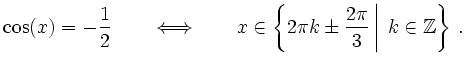
$\displaystyle \cos(x)=-\dfrac{1}{2} \qquad \Longleftrightarrow \qquad x\in \le... ...dfrac{2\pi}{3}}\vphantom{k\in\mathbb{Z}}\right.\, {k\in\mathbb{Z}}\right\} \,. $

Die zweite Ableitung an diesen Stellen ist

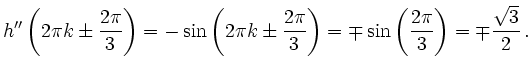
$\displaystyle h''\left(2\pi k \pm \dfrac{2\pi}{3}\right) =-\sin\left(2\pi k \pm... ...}{3}\right) =\mp \sin\left(\dfrac{2\pi}{3}\right) =\mp \dfrac{\sqrt{3}}{2} \,. $

An den Stellen $ x=2\pi k + 2\pi/3$ befinden sich also Hochpunkte, an $ x=2\pi k - 2\pi/3$ befinden sich Tiefpunkte mit den Funktionswerten

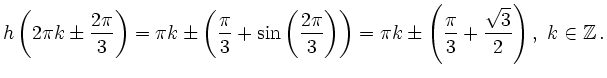
$\displaystyle h\left(2\pi k \pm \dfrac{2\pi}{3}\right) =\pi k \pm \left( \dfrac... ...\pm \left( \dfrac{\pi}{3} + \dfrac{\sqrt{3}}{2} \right), \ k\in\mathbb{Z} \,. $

Mit $ h''(x)=-\sin(x)=0$ genau dann, wenn $ x=k\pi$, $ k\in\mathbb{Z}$ und $ h'''(k\pi)=(-1)^{k+1}$ hat $ h$ die Wendepunkte

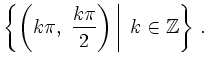
$\displaystyle \left\{{\left(k\pi,\ \dfrac{k\pi}{2}\right)}\left\vert\strut \vph... ...\pi}{2}\right)}\vphantom{k\in\mathbb{Z}}\right.\, {k\in\mathbb{Z}}\right\} \,. $

Abschließend gilt

$\displaystyle \lim\limits_{x\to-\infty}h(x)=-\infty$   und$\displaystyle \qquad \lim\limits_{x\to\infty}h(x)=+\infty \,. $

\includegraphics[width=0.8\linewidth]{h16_L_3.eps}
(Ackermann/Poppitz)
[Zurück zur Aufgabe]
  automatisch erstellt am 25.  8. 2006