Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
Mathematik-Online-Aufgabensammlung: Lösung zu

Aufgabe 1405: spezielle Integrale von trigonometrischen Funktionen

A B C D E F G H I J K L M N O P Q R S T U V W X Y Z
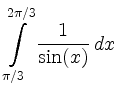Berechnen Sie die folgenden Integrale.
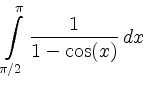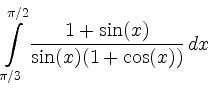
a) $ \displaystyle\int\limits_{\pi/3}^{2\pi/3} \frac{1}{\sin(x)}\, d x$                  b) $ \displaystyle\int\limits_{\pi/2}^{\pi} \frac{1}{1-\cos(x)}\, d x$                  c) $ \displaystyle\int\limits_{\pi/3}^{\pi/2} \frac{1+\sin(x)}{\sin(x)(1+\cos(x))}\, d x$
Mit Aufgabe 1438 erhält man
a)

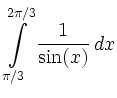$\displaystyle \int\limits_{\pi/3}^{2\pi/3} \frac{1}{\sin(x)}\, d x$ $\displaystyle =\int\limits_{u(\pi/3)}^{u(2\pi/3)}\frac{1}{u}\, d u =\bigg[\ln\v... ...g[{\ln}{\left({\tan}{\left(\frac{x}{2}\right)}\right)}\bigg]_{x=\pi/3}^{2\pi/3}$    
  $\displaystyle =\ln(3^{1/2})-\ln(3^{-1/2})=\ln(3)\,$,    

b)

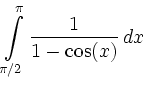$\displaystyle \int\limits_{\pi/2}^{\pi} \frac{1}{1-\cos(x)}\, d x$ $\displaystyle =\int\limits_{u(\pi/2)}^{u(\pi)} \frac{1}{u^2}\, d u =\left[-\fra... ...\to\pi-0}\left[-\frac{1}{{\tan}{\left(\frac{x}{2}\right)}}\right]_{x=\pi/2}^{t}$    
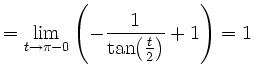  $\displaystyle =\lim_{t\to\pi-0}\left(-\frac{1}{{\tan}{\left(\frac{t}{2}\right)}}+1\right)=1\,$,    

c)

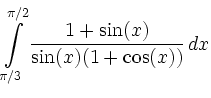$\displaystyle \int\limits_{\pi/3}^{\pi/2} \frac{1+\sin(x)}{\sin(x)(1+\cos(x))}\, d x$ $\displaystyle =\int\limits_{u(\pi/3)}^{u(\pi/2)}\frac{u}{2}+1+\frac{1}{2u}\, d u =\left[\frac{u^2}{4}+u+\frac{1}{2}\ln\vert u\vert\right]_{u(\pi/3)}^{u(\pi/2)}$    
  $\displaystyle =\left[\frac{\left({\tan}{\left(\frac{x}{2}\right)}\right)^2}{4}+... ...2}{\ln}{\left({\tan}{\left(\frac{x}{2}\right)}\right)}\right]_{x=\pi/3}^{\pi/2}$    
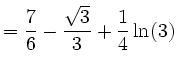  $\displaystyle =\frac{7}{6}-\frac{\sqrt{3}}{3}+\frac{1}{4}\ln(3)\,$.    

(Ackermann/Poppitz)
[Zurück zur Aufgabe]
  automatisch erstellt am 28.  8. 2006