
Mathematik-Online:

|
[Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen] |
|
Mathematik-Online: | |
Lineare Abbildungen und Darstellungsmatrizen |
| A B C D E F G H I J K L M N O P Q R S T U V W X Y Z | Übersicht |
Seien ![]() und
und ![]() Vektorräume über dem Körper
Vektorräume über dem Körper ![]() .
.
Begriff.
Eine Abbildung
![]() heißt linear, falls
heißt linear, falls
für alle
Ist ![]() und
und ![]() , und ist
, und ist
![]() eine Matrix, so ist zum Beispiel die Abbildung
eine Matrix, so ist zum Beispiel die Abbildung
linear.
Eine lineare Abbildung
![]() heißt auch Endomorphismus von
heißt auch Endomorphismus von ![]() .
.
Die Verkettung linearer Abbildungen ist wieder eine lineare Abbildung.
Ist
![]() eine lineare Abbildung, so ist
eine lineare Abbildung, so ist
ein Unterraum von
ein Unterraum von
Die lineare Abbildung ![]() ist injektiv genau dann, wenn
ist injektiv genau dann, wenn
![]() .
.
Ist die lineare Abbildung
![]() bijektiv, so ist auch die Umkehrabbildung
bijektiv, so ist auch die Umkehrabbildung
![]() wieder eine
lineare Abbildung.
wieder eine
lineare Abbildung.
Eine bijektive lineare Abbildung ![]() heißt auch Isomorphismus. Ein isomorpher Endomorphismus heißt auch
Automorphismus.
heißt auch Isomorphismus. Ein isomorpher Endomorphismus heißt auch
Automorphismus.
So etwa ist die identische Abbildung
![]() ein Isomorphismus.
ein Isomorphismus.
Kriterien.
Sei ![]() eine lineare Abbildung. Sei
eine lineare Abbildung. Sei
![]() eine Basis von
eine Basis von ![]() .
.
Die lineare Abbildung ![]() ist injektiv genau dann, wenn
ist injektiv genau dann, wenn
![]() linear unabhängig in
linear unabhängig in ![]() ist.
ist.
Die lineare Abbildung ![]() ist surjektiv genau dann, wenn
ist surjektiv genau dann, wenn
![]() erzeugend in
erzeugend in ![]() ist.
ist.
Die lineare Abbildung ![]() ist bijektiv genau dann, wenn
ist bijektiv genau dann, wenn
![]() eine Basis von
eine Basis von ![]() ist.
ist.
Dimensionsformel.
Sei
![]() eine lineare Abbildung. Dann gilt die Dimensionsformel
eine lineare Abbildung. Dann gilt die Dimensionsformel
Matrixmultiplikation.
Seien
![]() und
und
![]() Matrizen.
Das Matrixprodukt von
Matrizen.
Das Matrixprodukt von ![]() und
und ![]() ist definiert als
ist definiert als
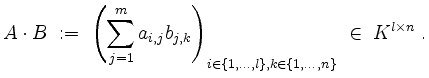
Der Eintrag an der Position
Ist
![]() , so setzen wir
, so setzen wir
![]() ,
, ![]() ,
,
![]() , ...,
, ...,
![]() .
.
Vorsicht! Es gilt i.a.
![]() für
für
![]() .
.
Darstellungsmatrix.
Sei
![]() eine lineare Abbildung.
Sei
eine lineare Abbildung.
Sei
![]() eine Basis von
eine Basis von ![]() , und sei
, und sei
![]() eine Basis von
eine Basis von ![]() .
.
Dann gibt es eindeutig bestimmte Koeffizienten
![]() in
in ![]() so, daß
so, daß
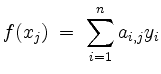
für alle
heißt die Darstellungsmatrix von
Kurz, die Spalten der Darstellungsmatrix sind die Koeffizienten der Bilder der Basisvektoren von ![]() bezüglich
der Basis von
bezüglich
der Basis von ![]() .
.
Ist ![]() ein weiterer Vektorraum über
ein weiterer Vektorraum über ![]() mit Basis
mit Basis
![]() , und ist
, und ist
![]() eine lineare Abbildung, so ist
eine lineare Abbildung, so ist
d.h. die Darstellungsmatrix der Verkettung ist gleich dem Matrixprodukt der Darstellungsmatrizen.
Ist ![]() ,
, ![]() , sind
, sind
![]() bzw.
bzw.
![]() die Standardbasen des
die Standardbasen des ![]() bzw.
bzw. ![]() , und ist
, und ist
![]() ,
,
![]() , wobei
, wobei
![]() , so ist
, so ist
d.h. die Multiplikation mit
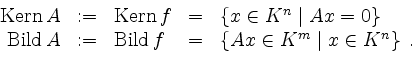
Rang einer Matrix.
Sei
![]() eine Matrix, und seien
eine Matrix, und seien
![]() die Spaltenvektoren von
die Spaltenvektoren von ![]() . Dann
ist der Rang von
. Dann
ist der Rang von ![]() definiert durch
definiert durch
Es ist
d.h.
Zur Berechnung des Rangs bringe man die Matrix ![]() in Zeilenstufenform. Der Rang ist dann gleich der Anzahl der Nichtnullzeilen
in der Zeilenstufenform.
in Zeilenstufenform. Der Rang ist dann gleich der Anzahl der Nichtnullzeilen
in der Zeilenstufenform.
Seien
![]() und
und
![]() Matrizen. Dann gilt
Matrizen. Dann gilt
Ist
![]() eine lineare Abbildung, und sind
eine lineare Abbildung, und sind
![]() bzw.
bzw.
![]() Basen von
Basen von ![]() bzw.
bzw. ![]() , so gilt
, so gilt
Invertierbarkeit.
Sei
![]() eine quadratische Matrix, d.h. ihre Spaltenzahl ist gleich ihrer Zeilenzahl.
eine quadratische Matrix, d.h. ihre Spaltenzahl ist gleich ihrer Zeilenzahl.
![]() heißt invertierbar oder regulär, falls es eine Matrix
heißt invertierbar oder regulär, falls es eine Matrix
![]() gibt so, daß
gibt so, daß
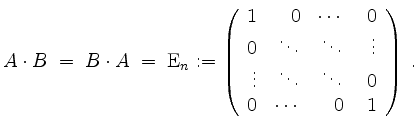
In diesem Falle ist die Matrix
Die Matrix ![]() heißt singulär, falls sie nicht regulär ist.
heißt singulär, falls sie nicht regulär ist.
Für eine quadratische Matrix
![]() sind folgende Aussagen äquivalent.
sind folgende Aussagen äquivalent.
Seien ![]() und
und ![]() Vektorräume derselben Dimension
Vektorräume derselben Dimension ![]() , seien
, seien
![]() bzw.
bzw.
![]() Basen von
Basen von ![]() bzw.
bzw. ![]() , und sei
, und sei
![]() eine lineare Abbildung. Dann sind folgende Aussagen äquivalent.
eine lineare Abbildung. Dann sind folgende Aussagen äquivalent.
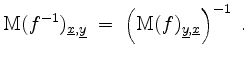
Berechnung der Inversen.
Sei
![]() eine quadratische Matrix.
eine quadratische Matrix.
Um ![]() auf Invertierbarkeit zu überprüfen und gegebenenfalls die Inverse von
auf Invertierbarkeit zu überprüfen und gegebenenfalls die Inverse von ![]() zu berechnen, wende man den Gaußschen Algorithmus
auf die folgende Matrix an.
zu berechnen, wende man den Gaußschen Algorithmus
auf die folgende Matrix an.
Hierbei kann ![]() in die Einheitsmatrix überführt werden genau dann, wenn
in die Einheitsmatrix überführt werden genau dann, wenn ![]() invertierbar ist. In diesem Falle entsteht in der rechten Hälfte
aus
invertierbar ist. In diesem Falle entsteht in der rechten Hälfte
aus
![]() die Inverse
die Inverse ![]() von
von ![]() .
.
siehe auch:
| automatisch erstellt am 22. 8. 2006 |