Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
Mathematik-Online:

Determinanten

A B C D E F G H I J K L M N O P Q R S T U V W X Y Z Übersicht

Permutationen.

Sei $ n\in\mathbb{N}$ . Eine Permutation von $ \{1,\ldots,n\}$ ist eine bijektive Abbildung $ \sigma:\{1,\ldots,n\}\longrightarrow\{1,\ldots,n\}$ . Wir schreiben sie als

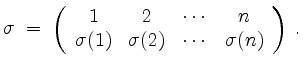
$\displaystyle \sigma \;=\; \left(\begin{array}{cccc}1 & 2 & \cdots & n \\ \sigma(1) & \sigma(2) & \cdots & \sigma(n)\end{array}\right)\;. $

Die identische Abbildung, die alle Zahlen in $ \{1,\ldots,n\}$ festläßt, wird mit $ \mathrm{id}_{\{1,\dots,n\}}$ oder kurz mit $ \mathrm{id}$ bezeichnet.

Die Menge aller Permutationen von $ \{1,\ldots,n\}$ wird mit $ \mathrm{Sym}_n$ bezeichnet. Sie enthält $ n!$ Elemente.

Zum Beispiel ist

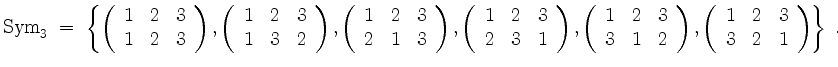
$\displaystyle \mathrm{Sym}_3 \;=\; \left\{ \left(\begin{array}{ccc} 1 & 2 & 3... ...(\begin{array}{ccc} 1 & 2 & 3\\ 3 & 2 & 1\\ \end{array}\right) \right\}\; . $

Zykelschreibweise.

Ein Zykel wird geschrieben als

$\displaystyle (a_1,a_2,\dots,a_k) $

mit paarweise verschiedenen $ a_i\in\{ 1,\dots, n\}$ , und bezeichnet die Permutation, welche $ a_i$ auf $ a_{i+1}$ schickt für $ i\in\{ 1,\dots,k-1\}$ , und $ a_k$ auf $ a_1$ , und die übrigen Elemente von $ \{1,\dots,n\}$ festläßt.

Zum Beispiel ist, in der Reihenfolge wie oben,

$\displaystyle \mathrm{Sym}_3 \;=\; \{\, \mathrm{id},\, (2,3),\, (1,2),\, (1,2,3),\, (1,3,2),\, (1,3)\,\}\; . $

Jede Permutation $ \sigma\in\mathrm{Sym}_n$ kann als Produkt paarweise disjunkter Zykel geschrieben werden. Zwei Zykel heißen hierbei disjunkt, falls sie kein gemeinsames Element aufweisen. Um diese Zykelschreibweise zu erhalten, verfahre man etwa wie folgt.

Sei $ b_1 = 1$ . Der erste Zykel ist gegeben durch

$\displaystyle (\sigma^0(b_1),\sigma^1(b_1),\sigma^2(b_1),\dots,\sigma^{k_1-1}(b_1))\; , $

wobei $ k_1\geq 1$ minimal sei mit $ \sigma^{k_1}(b_1) = b_1$ .

Sei $ b_2\in\{1,\dots,n\}$ minimal unter den Zahlen, die nicht im ersten Zykel auftreten. Der zweite Zykel ist gegeben durch

$\displaystyle (\sigma^0(b_2),\sigma^1(b_2),\sigma^2(b_2),\dots,\sigma^{k_2-1}(b_2))\; , $

wobei $ k_2\geq 1$ minimal sei mit $ \sigma^{k_2}(b_2) = b_2$ .

Sei $ b_3\in\{1,\dots,n\}$ minimal unter den Zahlen, die nicht in den ersten beiden Zykeln auftreten. Der dritte Zykel ist gegeben durch

$\displaystyle (\sigma^0(b_3),\sigma^1(b_3),\sigma^2(b_3),\dots,\sigma^{k_3-1}(b_3))\; , $

wobei $ k_3\geq 1$ minimal sei mit $ \sigma^{k_3}(b_3) = b_3$ .

Und so fort, bis nach dem $ l$ -ten Schritt alle Zahlen in $ \{1,\dots,n\}$ abgehandelt sind. Wir erhalten

$\displaystyle \sigma \;=\; (\sigma^0(b_1),\dots,\sigma^{k_1-1}(b_1))\circ (\si... ...ma^{k_2-1}(b_2))\circ\cdots\circ (\sigma^0(b_l),\dots,\sigma^{k_l-1}(b_l))\; . $

Da die Kompositionsreihenfolge wegen Disjunktheit der Zykel keine Rolle spielt, wird das Verknüpfungszeichen $ (\circ)$ auch gerne weggelassen.

$\displaystyle \sigma \;=\; (\sigma^0(b_1),\dots,\sigma^{k_1-1}(b_1)) (\sigma^0... ...\dots,\sigma^{k_2-1}(b_2))\cdots (\sigma^0(b_l),\dots,\sigma^{k_l-1}(b_l))\; . $

Zykel der Länge $ k_i = 1$ kann man unterschlagen.

So wird zum Beispiel

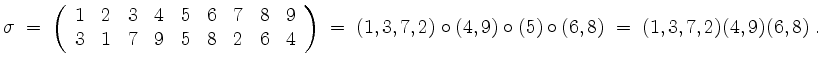
$\displaystyle \sigma \;=\; \left(\begin{array}{ccccccccc} 1 & 2 & 3 & 4 & 5 & 6... ...) \;=\; (1,3,7,2)\circ (4,9)\circ (5)\circ (6,8) \;=\; (1,3,7,2)(4,9)(6,8)\; . $

Signum.

Das Signum oder Vorzeichen einer Permutation

$\displaystyle \sigma \;=\; (\sigma^0(b_1),\dots,\sigma^{k_1-1}(b_1)) (\sigma^0... ...k_2-1}(b_2))\cdots (\sigma^0(b_l),\dots,\sigma^{k_l-1}(b_l)) \in\mathrm{Sym}_n $

ist gegeben durch

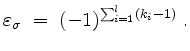
$\displaystyle \varepsilon_\sigma \;=\; (-1)^{\sum_{i = 1}^l (k_i - 1)}\; . $

In anderen Worten, ein Zykel gerader Länge hat negatives Vorzeichen, ein Zykel ungerader Länge hat positives Vorzeichen, und zur Bestimmung des Vorzeichens einer Permutation multipliziere man die Vorzeichen ihrer Zykel.

Es ist

$\displaystyle \varepsilon_{\sigma\circ\rho} \;=\; \varepsilon_\sigma\cdot\varepsilon_\rho $

für $ \sigma,\,\rho\,\in\,\mathrm{Sym}_n$ .

Definition der Determinante.

Sei $ K$ ein Körper, sei $ n\geq 1$ , und sei $ A = (a_{i,j})_{i,j}\in K^{n\times n}$ . Sei die Determinante von $ A$ definiert durch die Leibnizsche Formel

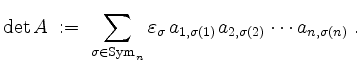
$\displaystyle \det A \; :=\; \sum_{\sigma\in\mathrm{Sym}_n} \varepsilon_\sigma\, a_{1,\sigma(1)} a_{2,\sigma(2)}\cdots a_{n,\sigma(n)}\; . $

Zum Beispiel ist für 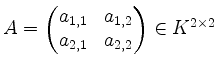$ A = \begin{pmatrix}a_{1,1}&a_{1,2}\\ a_{2,1}&a_{2,2}\end{pmatrix}\in K^{2\times 2}$ mit $ \tau:=(1,2)$

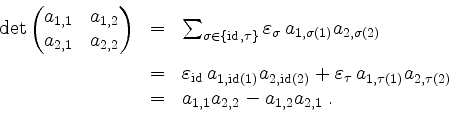
\begin{displaymath} \begin{array}{rcl} \det\begin{pmatrix}a_{1,1}&a_{1,2}\\ a_{2... ...\ & = & a_{1,1} a_{2,2} - a_{1,2} a_{2,1} \; . \\ \end{array}\end{displaymath}

Regeln.

Seien $ A,B\in K^{n\times n}$ . Dann ist

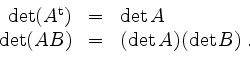
\begin{displaymath} \begin{array}{rcl} \det(A^\mathrm{t}) &=& \det A\\ \det(AB) &=& (\det A)(\det B)\;. \end{array}\end{displaymath}

Die Determinante einer oberen Blockdreiecksmatrix berechnet sich zu

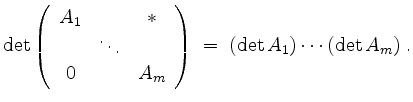
$\displaystyle \det\left(\begin{array}{ccc} A_1 & & \ast\\ & \ddots & \\ 0 & & A_m \end{array}\right) \;=\; (\det A_1)\cdots(\det A_m)\;. $

Dabei seien $ A_1,\ldots,A_m$ quadratische Matrizen beliebiger Größe.

Beachte insbesondere, daß für eine $ 1\times 1$ -Matrix $ A_i=(\alpha)\in K^{1\times 1}$ gilt, daß

$\displaystyle \det A_i \;=\; \alpha\;. $

Laplace-Entwicklung.

Sei

$\displaystyle A \;=\; (a_{i,j})_{i,j} \;\in\; K^{n\times n}\;. $

Für $ k,l\in\{1,\ldots,n\}$ bezeichne

$\displaystyle A_{k,l} \;:=\; (a_{i,j})_{i\in\{1,\ldots,k-1,\,k+1,\ldots,n\},\; j\in\{1,\ldots,l-1,\,l+1,\ldots,n\}} \;\in\; K^{(n-1)\times (n-1)} $

die Matrix, welche aus $ A$ hervorgeht durch Streichen der $ k$ -ten Zeile und der $ l$ -ten Spalte.

Die Determinante von $ A$ läßt sich durch die Laplace-Entwicklung nach der $ k$ -ten Zeile

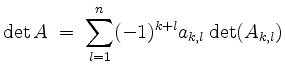
$\displaystyle \det A \;=\; \sum_{l=1}^n (-1)^{k+l} a_{k,l} \det(A_{k,l}) $

oder nach der $ l$ -ten Spalte

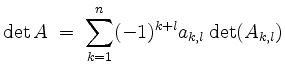
$\displaystyle \det A \;=\; \sum_{k=1}^n (-1)^{k+l} a_{k,l} \det(A_{k,l}) $

berechnen.

Gaußschritte.

Gaußsche Umformungen können verwendet werden, um eine Matrix $ A\in K^{n\times n}$ zwecks Determinantenberechnung zu vereinfachen.

Dasselbe gilt für Spaltenumformungen.

In der Praxis verwendet man häufig Gaußschritte zur Vorbereitung einer Laplace-Entwicklung durch weitgehendes Säubern einer Zeile oder einer Spalte.

Regularität, Cramer.

Sei $ A\in K^{n\times n}$ . Die Matrix $ A$ ist genau dann invertierbar, wenn $ \det A\ne 0$ .

Genauer, es gilt dann die Cramersche Regel,

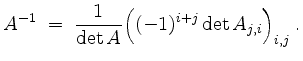
$\displaystyle A^{-1} \;=\; \frac{1}{\det A}\Big((-1)^{i+j}\det A_{j,i}\Big)_{i,j} \;. $

In der Praxis verwendet man diese Regel hauptsächlich zur Berechnung einzelner Einträge von $ A^{-1}$ .

Flächen- und Volumenberechnung.

Zwei Vektoren 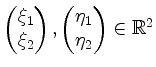$ \begin{pmatrix}\xi_1 \\ \xi_2\end{pmatrix},\begin{pmatrix}\eta_1 \\ \eta_2\end{pmatrix}\in\mathbb{R}^2$ spannen ein Parallelogramm

$\displaystyle \{\lambda\begin{pmatrix}\xi_1 \\ \xi_2\end{pmatrix}+\mu\begin{pmatrix}\eta_1 \\ \eta_2\end{pmatrix}\;\vert\; \lambda,\mu\in[0,1]\} $

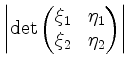auf. Sein Flächeninhalt ist gegeben durch $ \left\vert\det\begin{pmatrix}\xi_1&\eta_1\\ \xi_2&\eta_2\end{pmatrix}\right\vert$ .

Drei Vektoren 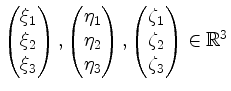$ \begin{pmatrix}\xi_1\\ \xi_2\\ \xi_3\end{pmatrix},\begin{pmatrix}\eta_1\\ \eta... ...pmatrix},\begin{pmatrix}\zeta_1\\ \zeta_2\\ \zeta_3\end{pmatrix}\in\mathbb{R}^3$ spannen ein Parallelotop

$\displaystyle \{\lambda\begin{pmatrix}\xi_1\\ \xi_2\\ \xi_3\end{pmatrix}+\mu\be... ...ix}\zeta_1\\ \zeta_2\\ \zeta_3\end{pmatrix}\;\vert\; \lambda,\mu,\nu\in[0,1]\} $

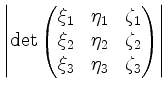auf. Sein Volumen ist gegeben durch $ \left\vert\det\begin{pmatrix}\xi_1&\eta_1&\zeta_1\\ \xi_2&\eta_2&\zeta_2\\ \xi_3&\eta_3&\zeta_3\end{pmatrix}\right\vert$ .

Allgemeiner, sei $ A\in\mathbb{R}^{n\times k}$ mit $ k\leq n$ . Das von den Spaltenvektoren von $ A$ aufgespannte $ k$ -Parallelotop

$\displaystyle \{A\cdot\begin{pmatrix}\lambda_1\\ \vdots\\ \lambda_k\end{pmatrix}\;\vert\; \lambda_1,\ldots,\lambda_k\in[0,1]\}\subseteq\mathbb{R}^n $

hat das $ k$ -dimensionale Volumen $ \sqrt{\det(A^\mathrm{t}A)}$ .

Ist speziell $ k=2$ und $ n=3$ , so ist dieses Volumen gleich $ \Vert a_1\times a_2\Vert$ , wobei $ A=(a_1,a_2)$ mit $ a_1,a_2\in\mathbb{R}^3$ sei.

(Autoren: Künzer/Martin/Tentler/Wahrheit)

Beispiele:

[Verweise]
  automatisch erstellt am 11.  8. 2006