Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
Mathematik-Online:

Stetigkeit

A B C D E F G H I J K L M N O P Q R S T U V W X Y Z Übersicht

Norm, Folgenkonvergenz und Abschluß.

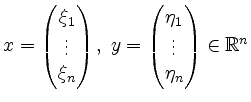Seien $ l,\, m,\, n,\, n\,\ge\, 1$ . Seien $ x = \begin{pmatrix} \xi_1\\ \vdots\\ \xi_n \end{pmatrix},\; y = \begin{pmatrix} \eta_1\\ \vdots\\ \eta_n \end{pmatrix} \in \mathbb{R}^n$ .

Wir erinnern an das Skalarprodukt $ x^\mathrm{t} y = \xi_1 \eta_1 + \cdots + \xi_n \eta_n$ und die (euklidische) Norm $ \Vert x \Vert = \sqrt{x^\mathrm{t} x} = \sqrt{ \xi_1^2 + \cdots + \xi_n^2}$ .

Die (euklidische) Norm erfüllt folgende drei Eigenschaften für alle $ x,y \in \mathbb{R}^n, \alpha \in \mathbb{R}$ :

Eine Folge $ (x_k)_{k\ge 1}$ konvergiert gegen einen Punkt $ x\in\mathbb{R}^n$ , wenn für alle $ \varepsilon>0$ ein $ N\ge 1$ so existiert, daß

$\displaystyle \Vert x_k-x\Vert<\varepsilon \hspace*{1cm}$   $\displaystyle \mbox{f''ur alle $k\ge N$}$$\displaystyle \; , $

d.h. falls $ \Vert x_k - x \Vert \to 0$ für $ k\to\infty$ . Der Punkt $ x$ heißt dann der Grenzwert der Folge $ (x_k)_{k\ge 1}$ .

Schreibweise: $ x = \displaystyle\lim_{k\to\infty} x_k$ oder $ x_k \to x$ .

Der Grenzwert einer Folge ist eindeutig bestimmt, falls er existiert.

Es sei $ D \subseteq \mathbb{R}^n$ . Ein Punkt $ x_0 \in \mathbb{R}^n$ heißt Berührpunkt von $ D$ , falls für jedes $ \varepsilon>0$ die (offene) $ \varepsilon$ -Umgebung

$\displaystyle B_\varepsilon(x_0) := \{ x \in \mathbb{R}^n \vert \; \Vert x - x_0 \Vert < \varepsilon \} $

mit $ D$ nichtleeren Schnitt hat. Die Menge aller Berührpunkte von $ D$ heißt der Abschluß von $ D$ und wird mit $ \bar{D}$ bezeichnet. Dies ist zugleich die Menge aller Punkte $ x\in\mathbb{R}^n$ derart, daß eine Folge mit Folgegliedern in $ D$ existiert, die gegen $ x$ konvergiert.

Funktionsgrenzwerte.

Sei $ D \subseteq \mathbb{R}^n$ eine Teilmenge, und sei $ f:D\to\mathbb{R}^m$ eine Funktion.

Es heißt $ y_0\in\mathbb{R}^m$ der Grenzwert von $ f$ an der Stelle $ x_0\in\bar{D}$ , falls es für alle $ \varepsilon>0$ ein $ \delta > 0$ gibt mit

$\displaystyle \Vert f(x) - y_0\Vert \; < \; \varepsilon $

für alle $ x\in D$ mit

$\displaystyle \Vert x - x_0\Vert\; < \; \delta\; . $

In anderen Worten, für alle $ \varepsilon>0$ gibt es ein $ \delta > 0$ so, daß

$\displaystyle f(B_\delta(x_0)\cap D) \;\subseteq\; B_\varepsilon(y_0) \; . $

Existiert der Grenzwert $ y_0$ bei $ x_0$ , dann sagen wir, $ f$ konvergiert an der Stelle $ x_0$ gegen $ y_0$ , und schreiben

$\displaystyle \lim_{x\to x_0} f(x) \; := \; y_0\; . $

Nach dem Folgenkriterium konvergiert $ f(x)$ gegen $ y_0$ an der Stelle $ x_0$ , falls für alle Folgen $ (x_k)_{k\ge 1}$ mit $ x_k\in D$ und $ x_k\to x_0$ gilt, daß $ f(x_k)\to y_0$ .

Stetigkeit.

Sei $ D \subseteq \mathbb{R}^n$ eine Teilmenge, und sei $ f:D\to\mathbb{R}^m$ eine Funktion.

Die Funktion $ f$ heißt stetig im Punkt $ x_0\in D$ , wenn

$\displaystyle \lim_{x\to x_0}f(x)=f(x_0)\;, $

d.h. wenn dieser Grenzwert existiert.

Die Funktion $ f$ heißt stetig, wenn sie in allen Punkten $ x_0\in D$ stetig ist.

Ist 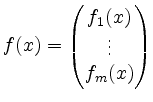$ f(x)=\begin{pmatrix}f_1(x)\\ \vdots\\ f_m(x)\end{pmatrix}$ mit Koordinatenfunktionen $ f_1,\,\ldots,\,f_m\, :\,D\to\mathbb{R}$ , so ist $ f$ stetig in $ x_0$ genau dann, wenn $ f_1,\ldots,f_m$ stetig in $ x_0$ sind.

Ist $ f:\mathbb{R}^n\to\mathbb{R}$ ein Polynom, d.h. gilt

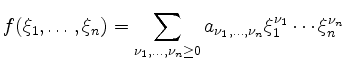
$\displaystyle f(\xi_1,\ldots,\xi_n) = \sum_{\nu_1,\ldots,\nu_n \geq 0} a_{\nu_1,\ldots,\nu_n}\xi_1^{\nu_1}\cdots\xi_n^{\nu_n} $

mit Koeffizienten $ a_{\nu_1,\ldots,\nu_n}\in\mathbb{R}$ und $ a_{\nu_1,\ldots,\nu_n}\ne 0$ nur für endlich viele $ \nu_1,\ldots,\nu_n\geq 0$ , so ist $ f$ stetig.

Für stetige Funktionen $ f,g: D \to \mathbb{R}^m$ , $ h:E \to D$ , wobei $ E \subseteq \mathbb{R}^l$ , sowie $ \alpha, \beta \in \mathbb{R}$ , sind auch die Funktionen

$\displaystyle \alpha f + \beta g\; , \hspace*{1cm} f^\mathrm{t} g\; , \hspace*{1cm} f \circ h $

stetig.

Satz von Weierstraß.

Eine Teilmenge $ K\subseteq\mathbb{R}^n$ heißt abgeschlossen, falls $ K=\bar{K}$ , d.h. falls $ K$ alle seine Berührpunkte enthält.

Die Menge $ K$ heißt beschränkt, falls $ \sup\{\Vert x\Vert\,\vert\, x\in K\}<\infty$ , d.h. falls es ein $ c>0$ gibt, so daß $ \Vert x\Vert\leq c$ für alle $ x\in K$ .

Die Menge $ K$ heißt kompakt, falls sie abgeschlossen und beschränkt ist.

Sei $ f:K\to\mathbb{R}$ eine stetige Funktion auf einer nicht-leeren kompakten Menge $ K\subseteq\mathbb{R}^n$ . Dann existieren nach dem Satz von Weierstraß $ \min f(K)$ und $ \max f(K)$ , d.h. es gibt $ x_0,\, x_1\,\in\, K$ , so daß

$\displaystyle \min f(K) \; =\; f(x_0) \;\leq\; f(x) \;\leq\; f(x_1)\; =\; \max f(K) \hspace*{1cm}$$\displaystyle \mbox{f''ur alle $x\in K$}$$\displaystyle \;. $

Kurz, eine stetige Funktion $ f$ nimmt auf einem Kompaktum $ K$ Maximum und Minimum an.

Satz von Heine-Borel.

Es sei $ M\subseteq\mathbb{R}^n$ eine Teilmenge. Unter einer offenen Überdeckung von $ M$ versteht man eine Familie $ (U_i)_{i\in I}$ von offenen Mengen $ U_i\subseteq\mathbb{R}^n$ derart, daß

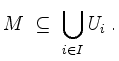
$\displaystyle M \;\subseteq\; \bigcup_{i\in I} U_i\;. $

Unter einer Teilüberdeckung der Familie $ (U_i)_{i\in I}$ versteht man eine offene Überdeckung von $ U$ der Form $ (U_i)_{i\in I_0}$ , wobei $ I_0\subseteq I$ eine Teilmenge ist. Die Teilüberdeckung $ (U_i)_{i\in I_0}$ heißt endlich, falls die Indexmenge $ I_0$ endlich viele Elemente hat.

Der Satz von Heine-Borel besagt nun, daß die Menge $ M$ genau dann kompakt ist, wenn jede offene Überdeckung von $ M$ eine endliche Teilüberdeckung besitzt.

(Autoren: Künzer/Martin/Tentler/Wahrheit)

Beispiele:

[Verweise]
  automatisch erstellt am 11.  8. 2006